§６．扇型磁極面により作られる磁界

1)磁界の表式

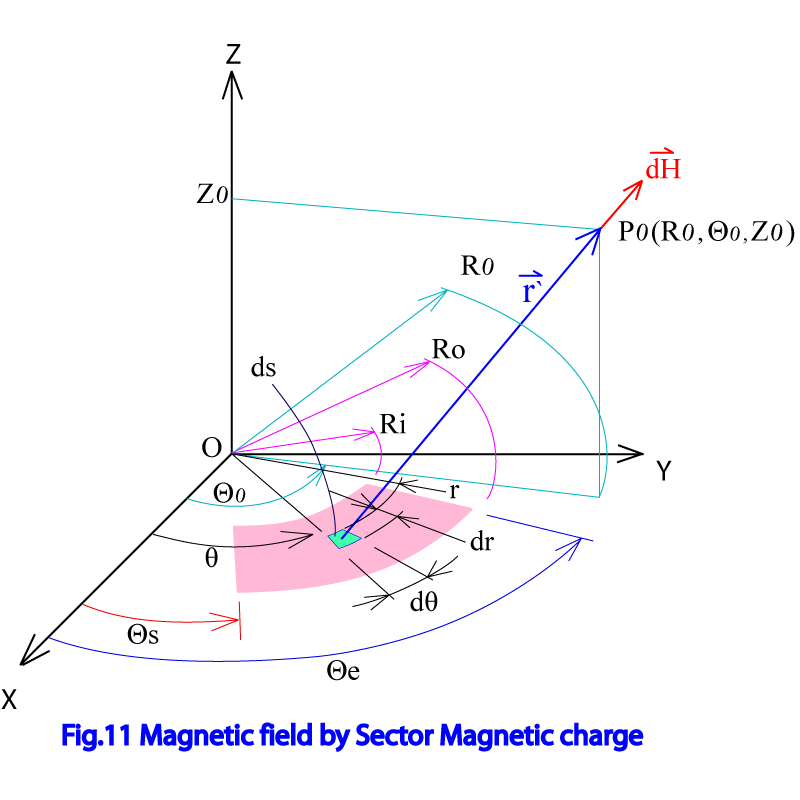
Fig.11で示されたように固有座標径に於いて、開き開始角度Θsから終了角度Θe、内径Ri、外径Roで定義された扇型の磁極面が円筒座標系の点　P(R0 , Θ0 , Z0 )　に作る磁界を計算する。 円筒座標径で、扇型上の点（r , θ , 0）に位置し微小角度dθ、微小径方向長さdrを持った微小要素を　ds　とする。　座標原点O からdsまでのベクトル　r⃑　はX-Y-Z座標系で表すと、

r⃑= (rcos⁡θ , rsin⁡θ , 0 )

またdsの面積は

ds=r dθ dr

となる。また、dsから点P0迄を結んだベクトルを　r`⃑　とすると、

r` ⃑= ( R0 cos⁡Θ0- rsin⁡θ, R0 sin⁡Θ0- rsin⁡Θ0- rsin⁡θ , Z 0)

となり、距離　r` は

r'= r` ⃑･r`⃑ = r2 - 2R 0r cos⁡Θ0- θ + R02 + Z02 式(6-1)

となる。

また微小要素の磁極面の磁荷　dm は、磁石の残留磁束密度をBr とすると

dm = Br ds

微小要素dsによって点P0に作られる磁界 dH⃑ はdsから点P0を結ぶ方向を向いたベクトルで 以下の様に表せる。

dH⃑ = Br ds4π μ0 r`2 r`⃑r`

従って、全ての扇型磁極面からの磁界H⃑への寄与は扇型全体に積分する事により求められ

H⃑ = 14πμ0 ∫RiRo∫ΘsΘeBrr`2 r`⃑r` r dθ dr

となる。これをH⃑の各成分で表せば

Hx= Br4πμ0∫RiRo∫ΘsΘe1r`3 R0 cos⁡Θ0- r cos⁡θ r dr dθ 式(6-2)

Hy = Br4πμ0∫RiRo∫ΘsΘe1r`3 R0 sin⁡Θ0⁡- r sin⁡θ r dr dθ 式(6-3)

HZ = Br4πμ0∫RiRo∫ΘsΘe1r`3 Z0 r dr dθ 式(6-4)

となる。