§8-1.Mag field by straight square current(Delive equation)

§８．直線平角ワイヤーに流れる電流により作られる磁界

1)磁界の表式

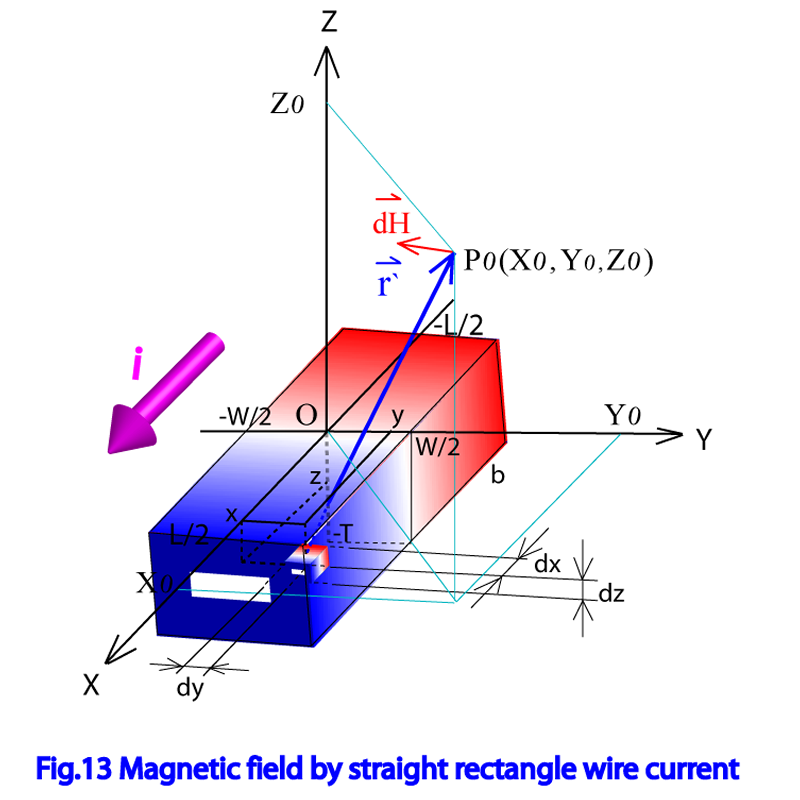
直線平角導線に流れる電流により作られる磁場

Fig.13に示された様に、X軸方向に－L/2からL/2まで伸び、Y軸方向の幅がW（－W/2からW/2）、Z軸の厚さがT（－Tから0）である直線四角型の導線に、電流密度i の電流ががX軸方向に流れている時、点 $P_{0}$ に作られる磁界 $\overset{⃑}{H}$ を考える。

先ず、位置（x¸y¸z）にある微小電流要素（dx¸dy¸dz）が点　 $P_{0}$ 　に作る磁界を　 $\overset{⃑}{d H}$ 　とするとビオサバールの法則より

$\overset{⃑}{d H} = \frac{1}{4 π} \frac{i ∙ d y ∙ d z ∙ \overset{⃑}{d x} \times \overset{⃑}{r'}}{{r'}^{3}}$ 式(8-1)

ここで　 $\overset{⃑}{r}'$ は微小要素から点 $P_{0} (X_{0}, Y_{0,} Z_{0})$ までのベクトルで

$\overset{⃑}{r `} = (X_{0} - x, Y_{0} - y, Z_{0} - z)$ 式(8-2)

また

$\overset{⃑}{d x} = (d x, 0, 0)$

であるから

$\overset{⃑}{d x} \times \overset{⃑}{r `} = - d x (Z_{0} - z) \overset{⃑}{e_{y}} + d x (Y_{0} - y) \overset{⃑}{e_{z}}$ 式(8-3)

と表せる。ここで $\overset{⃑}{e_{y}}, \overset{⃑}{e_{z}}$ は夫々　Y　軸、Z軸　方向の単位ベクトルとする。従って　式(8-1)　の　 $\overset{⃑}{d H}$ の各成分は

${d H}_{x} = 0$ 式(8-4)

$d H_{y} = - \frac{i}{4 π} \frac{1}{{r'}^{3}} (Z_{0} - z) d x d y d z$ 式(8-5)

$d H_{z} = \frac{i}{4 π} \frac{1}{{r'}^{3}} (Y_{0} - y) d x d y d z$ 式(8-6)

と表せる。　従って　磁界は上記の微小電流の寄与を全ての電流の範囲に渡って積分することにより求まり以下のように表す事ができる。

$H_{x} = 0$ 式(8-7)

$H_{y} = - \frac{i}{4 π} \int_{- \frac{L}{2}}^{\frac{L}{2}} d x \int_{- \frac{w}{2}}^{\frac{w}{2}} d y \int_{- T}^{0} d z \frac{Z_{0} - z}{{\sqrt{{({x - X}_{0})}^{2} + {(y - Y_{0})}^{2} + {(z - Z_{0})}^{2}}}^{3}}$ 式(8-8)

$H_{z} = \frac{i}{4 π} \int_{- \frac{L}{2}}^{\frac{L}{2}} d x \int_{- \frac{w}{2}}^{\frac{w}{2}} d y \int_{- T}^{0} d z \frac{Y_{0} - y}{{\sqrt{{({x - X}_{0})}^{2} + {(y - Y_{0})}^{2} + {(z - Z_{0})}^{2}}}^{3}}$ 式(8-9)

Publication Date：16May2015 　　　　updated：31Jan2018
Author：Nobuo Kojima
Mail To：
2011-2020 Copyright by Kojimag