§1-2)Magnetic Dipole

§1.THE MAGNETIC FIELD INCLUDING MAGNETIZED MATERIAL

2)Magnetic field by magnetic dipole

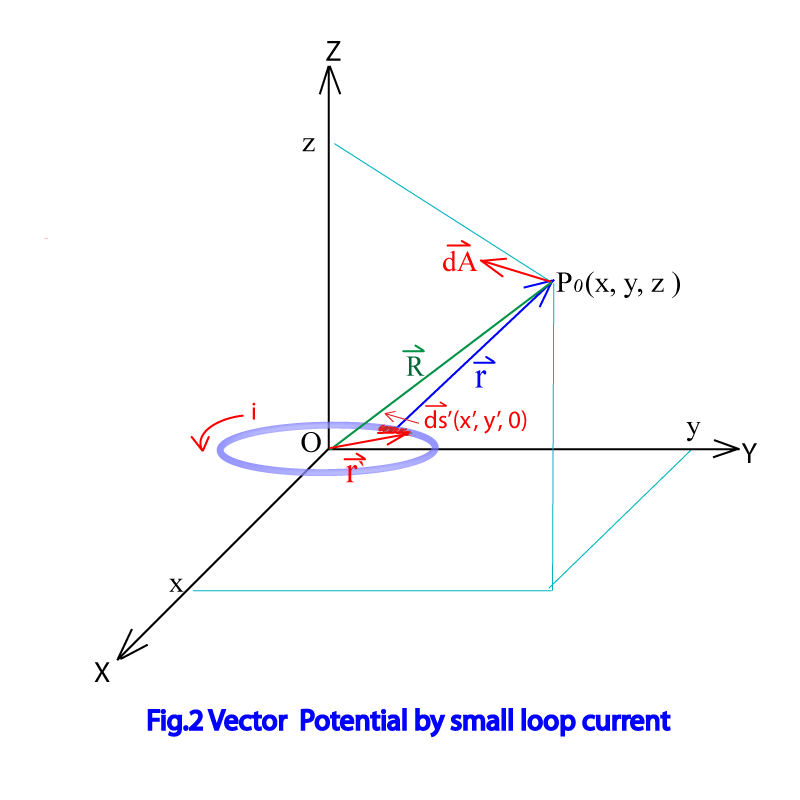
Vector potential by circulation currets

Consider small circulation current as shown in Fig.2 , assuming constant current i in it, and located on the xy plane. Assuming $\overset{⃑}{d s'}$ as small vector element of the circulation current located position $\overset{⃑}{r'} (x', y', 0)$ .
Then the vector potential at the position $P_{0} (x, y, z)$ become

$\overset{⃑}{A} = \frac{μ_{0}}{4 π} ∭ \frac{\overset{⃑}{ｉ}}{r} d V' = \frac{μ_{0} ｉ}{4 π} \oint \frac{\overset{⃑}{d s}'}{r}$ Eq.(1-7)

Here,

$\overset{⃑}{r} = (x - x^{'}, y - y^{'}, z), r = \sqrt{{(x - x^{'})}^{2} + {(y - y^{'})}^{2} + z^{2}}$ Eq.(1-8)

And

$\overset{⃑}{R} = (x, y, z), R = \sqrt{x^{2} + y^{2} + z^{2}}$ Eq.(1-9)

If assuming the size of circulation current dimension much smaller than the distance until point $P_{0}$ . Then we can consider , $R ≫ x^{'}, R ≫ y'$

So we can approximate r using until power of x'/R and y'/R.
Then Eq.(1-8) is

$r = {[(x^{2} + y^{2} + z^{2}) \{1 - 2 (\frac{{x x}^{'} - \frac{{x^{'}}^{2}}{2}}{x^{2} + y^{2} + z^{2}}) - 2 (\frac{{y y}^{'} - \frac{{y^{'}}^{2}}{2}}{x^{2} + y^{2} + z^{2}})\}]}^{\frac{1}{2}}$

$= R \sqrt{1 - 2 (x x' - \frac{{x'}^{2}}{2}) / R^{2} - 2 (y y' - \frac{{y'}^{2}}{2}) / R^{2}} ≅ R (1 - x x' / R^{2} - y y' / R^{2})$ Eq.(1-10)

Therefore 1/r become

$\frac{1}{r} = \frac{1}{R (1 - x x' / R^{2} - y y' / R^{2})} ≅ \frac{1}{R} \{1 + \frac{1}{R^{2}} (x x' + y y')\}$ Eq.(1-11)

$\overset{⃑}{A} = \frac{μ_{0} ｉ}{4 π} \oint \frac{\overset{⃑}{d s'}}{r} ≅ \frac{μ_{0} ｉ}{4 π} \frac{1}{R} \oint \{1 + \frac{1}{R^{2}} (x x' + y y')\} \overset{⃑}{d s}'$ Eq.(1-12)

Here first term of path integral become zero and the integral of second term become below.

$\overset{⃑}{A} = \frac{μ_{0} ｉ}{4 π} \frac{1}{R^{3}} \oint ({x x}^{'} + {y y}^{'}) \overset{⃑}{d s}' = \frac{μ_{0} ｉ}{4 π} \frac{1}{R^{3}} (x \oint x' \overset{⃑}{d s} + y \oint y' \overset{⃑}{d s})$ Eq.(1-13)

Here in Eq.(1-13), path integral of first term will beexpressed as

$\oint x' \overset{⃑}{d s} = \oint x' {d s'}_{x} \overset{⃑}{e_{x}} + \oint x' {d s'}_{y} \overset{⃑}{e_{y}}$

First term of this path integral go and back on the x axis for the same $x'$ value it's sign of ${d s'}_{x}$ is opposite , so integral become zero(refer Fig.3). Second integral become surface area S surrounded by path(refer Fig.3).
Then second term in path integral of Eq.(1-13) is

$\oint y' \overset{⃑}{d s} = \oint y' {d s'}_{x} \overset{⃑}{e_{x}} + \oint y' {d s'}_{y} \overset{⃑}{e_{y}}$

Here first term become surface area S surrounded by path.(refer Fig.3) And second term become zero because go and back on the y axis for same $y'$ value the sign of ${d s'}_{y}$ become opposite. Therefore Eq.(1-13) become

$\overset{⃑}{A} = \frac{μ_{0} ｉ}{4 π} \frac{1}{R^{3}} (x \oint x' \overset{⃑}{d s'} + y \oint y' \overset{⃑}{d s'}) = \frac{μ_{0} ｉ}{4 π} \frac{1}{R^{3}} (x S \overset{⃑}{e_{y}} - y S \overset{⃑}{e_{x}})$

$= \frac{μ_{0} ｉ}{4 π} \frac{S}{R^{3}} (x \overset{⃑}{e_{y}} - y \overset{⃑}{e_{x}}) = \frac{μ_{0} ｉ}{4 π} \frac{S}{R^{3}} (x \overset{⃑}{e_{z}} \times \overset{⃑}{e_{x}} - y \overset{⃑}{e_{y}} \times \overset{⃑}{e_{z}})$

$= \frac{μ_{0} ｉ}{4 π} \frac{S}{R^{3}} \overset{⃑}{e_{z}} \times (x \overset{⃑}{e_{x}} + y \overset{⃑}{e_{y}})$ Eq.(1-14)

Here we used that the vector product $\overset{⃑}{e_{y}} \times \overset{⃑}{e_{z}} = - \overset{⃑}{e_{z}} \times \overset{⃑}{e_{y}}$ . And also using $\overset{⃑}{e_{z}} \times \overset{⃑}{e_{z}} = 0$ , add $z (\overset{⃑}{e_{z}} \times \overset{⃑}{e_{z}})$ in the right hand of Eq.(1-14)

$\overset{⃑}{A} = \frac{μ_{0} ｉ}{4 π} \frac{S}{R^{3}} \overset{⃑}{e_{z}} \times (x \overset{⃑}{e_{x}} + y \overset{⃑}{e_{y}} + z \overset{⃑}{e_{z}}) = \frac{μ_{0} ｉ}{4 π} \frac{S}{R^{3}} \overset{⃑}{e_{z}} \times \overset{⃑}{R}$ Eq.(1-15)

Here we define below quantity as magnetic dipole moment.

$\overset{⃑}{m} = i S \overset{⃑}{e_{z}} = i \overset{⃑}{S}$ Eq.(1-16)

Here $\overset{⃑}{S}$ is the vector of which magnitude is S and normal direction of it's surface. Eq.(1-15) is expressed using this magnetic dipole moment $\overset{⃑}{m}$

$\overset{⃑}{A} = \frac{μ_{0}}{4 π} \frac{1}{R^{3}} \overset{⃑}{m} \times \overset{⃑}{R}$ Eq.(1-17)

Thus we could get equation of vector potential sourced by magnetic dipole moment at the position $\overset{⃑}{R}$
At first we assumed current is located on the XY surface, but Eq.(1-17) is generally applicable. We could get magnetic field by the rotation of Eq.(1-17). If using vector analysis general formula,

$\overset{⃑}{\nabla} \times (\overset{⃑}{F} \times \overset{⃑}{G}) = \overset{⃑}{F} (\overset{⃑}{\nabla} ∙ \overset{⃑}{G}) - \overset{⃑}{G} (\overset{⃑}{\nabla} ∙ \overset{⃑}{F}) + (\overset{⃑}{G} ∙ \overset{⃑}{\nabla}) \overset{⃑}{F} - (\overset{⃑}{F} ∙ \overset{⃑}{\nabla}) \overset{⃑}{G}$ Eq.(1-18)

$\overset{⃑}{m}$ is constant so $\overset{⃑}{\nabla} ∙ \overset{⃑}{m} = 0, (\frac{\overset{⃑}{R}}{R^{3}} ∙ \overset{⃑}{\nabla}) \overset{⃑}{m} = 0$ . Therefore the rotation of Eq.(1-17) is

$\overset{⃑}{B} = \overset{⃑}{\nabla} \times \overset{⃑}{A} = \frac{μ_{0}}{4 π} \overset{⃑}{\nabla} \times (\overset{⃑}{m} \times \frac{\overset{⃑}{R}}{R^{3}}) = \frac{μ_{0}}{4 π} \{\overset{⃑}{m} (\overset{⃑}{\nabla} ∙ \frac{\overset{⃑}{R}}{R^{3}}) - (\overset{⃑}{m} ∙ \overset{⃑}{\nabla}) \frac{\overset{⃑}{R}}{R^{3}}\}$

$= \frac{μ_{0}}{4 π} \{\overset{⃑}{m} (\frac{\partial}{\partial x} \frac{x}{{\sqrt{x^{2} + y^{2} + z^{2}}}^{3}} + \frac{\partial}{\partial y} \frac{y}{{\sqrt{x^{2} + y^{2} + z^{2}}}^{3}} + \frac{\partial}{\partial z} \frac{z}{{\sqrt{x^{2} + y^{2} + z^{2}}}^{3}})\}$

$- \frac{μ_{0}}{4 π} \{(m_{x} \frac{\partial}{\partial x} \frac{x}{{\sqrt{x^{2} + y^{2} + z^{2}}}^{3}} + m_{y} \frac{\partial}{\partial y} \frac{x}{{\sqrt{x^{2} + y^{2} + z^{2}}}^{3}} + m_{z} \frac{\partial}{\partial z} \frac{x}{{\sqrt{x^{2} + y^{2} + z^{2}}}^{3}}) \overset{⃑}{e_{x}}$

$+ (m_{x} \frac{\partial}{\partial x} \frac{y}{{\sqrt{x^{2} + y^{2} + z^{2}}}^{3}} + m_{y} \frac{\partial}{\partial y} \frac{y}{{\sqrt{x^{2} + y^{2} + z^{2}}}^{3}} + m_{z} \frac{\partial}{\partial z} \frac{y}{{\sqrt{x^{2} + y^{2} + z^{2}}}^{3}}) \overset{⃑}{e_{y}}$

$+ (m_{x} \frac{\partial}{\partial x} \frac{z}{{\sqrt{x^{2} + y^{2} + z^{2}}}^{3}} + m_{y} \frac{\partial}{\partial y} \frac{z}{{\sqrt{x^{2} + y^{2} + z^{2}}}^{3}} + m_{z} \frac{\partial}{\partial z} \frac{z}{{\sqrt{x^{2} + y^{2} + z^{2}}}^{3}}) \overset{⃑}{e_{z}}\}$ Eq.(1-19)

Here first term in the { } become zero as below.

$\frac{\partial}{\partial x} \frac{x}{{\sqrt{x^{2} + y^{2} + z^{2}}}^{3}} + \frac{\partial}{\partial y} \frac{y}{{\sqrt{x^{2} + y^{2} + z^{2}}}^{3}} + \frac{\partial}{\partial z} \frac{z}{{\sqrt{x^{2} + y^{2} + z^{2}}}^{3}} = \frac{3}{{\sqrt{x^{2} + y^{2} + z^{2}}}^{3}} - \frac{3 (x^{2} + y^{2} + z^{2})}{{\sqrt{x^{2} + y^{2} + z^{2}}}^{5}}$

$= \frac{3}{{\sqrt{x^{2} + y^{2} + z^{2}}}^{3}} - \frac{3}{{\sqrt{x^{2} + y^{2} + z^{2}}}^{3}} = 0$ Eq.(1-20)

Second term in the ｛　｝, consider first（　）（x component）

$(m_{x} \frac{\partial}{\partial x} \frac{x}{{\sqrt{x^{2} + y^{2} + z^{2}}}^{3}} + m_{y} \frac{\partial}{\partial y} \frac{x}{{\sqrt{x^{2} + y^{2} + z^{2}}}^{3}} + m_{z} \frac{\partial}{\partial z} \frac{x}{{\sqrt{x^{2} + y^{2} + z^{2}}}^{3}})$

$= m_{x} (\frac{1}{{\sqrt{x^{2} + y^{2} + z^{2}}}^{3}} - \frac{3 x^{2}}{{\sqrt{x^{2} + y^{2} + z^{2}}}^{5}}) {- m}_{y} \frac{3 x y}{{\sqrt{x^{2} + y^{2} + z^{2}}}^{5}} {- m}_{z} \frac{3 x z}{{\sqrt{x^{2} + y^{2} + z^{2}}}^{5}}$

$= \frac{m_{x}}{{\sqrt{x^{2} + y^{2} + z^{2}}}^{3}} - \frac{3 x (m_{x} x + m_{y} y + m_{z} z)}{{\sqrt{x^{2} + y^{2} + z^{2}}}^{5}} = \frac{m_{x}}{R^{3}} - \frac{3 x \overset{⃑}{m} ∙ \overset{⃑}{R}}{R^{5}}$ Eq.(1-21)

So Eq.(1-19) become

$\overset{⃑}{B} = \frac{μ_{0}}{4 π} \{- \frac{\overset{⃑}{m}}{R^{3}} + \frac{3 \overset{⃑}{R} (\overset{⃑}{m} ∙ \overset{⃑}{R})}{R^{5}}\}$ Eq.(1-22)

Here we can express as below,

$\frac{\partial}{\partial x} (\frac{\overset{⃑}{m} ∙ \overset{⃑}{R}}{R^{3}}) = \frac{\partial}{\partial x} (\frac{m_{x} x + m_{y} y + m_{z} z}{{\sqrt{x^{2} + y^{2} + z^{2}}}^{3}}) = \frac{m_{x}}{{\sqrt{x^{2} + y^{2} + z^{2}}}^{3}} - \frac{3 x (m_{x} x + m_{y} y + m_{z} z)}{{\sqrt{x^{2} + y^{2} + z^{2}}}^{5}}$ Eq.(1-23)

Therefore Eq.(1-22) conclude as below.

$\overset{⃑}{B} = - μ_{0}$ $\overset{⃑}{\nabla} (\frac{\overset{⃑}{m} ∙ \overset{⃑}{R}}{{4 π R}^{3}})$ Eq.(1-24)

Publication Date：16May2015 　　　　updated：27Jan2018
Author：Nobuo Kojima
Mail To：
2011-2020 Copyright by Kojimag