§1-3)The case including magnetized material(vector potential equation)

§1.The case including magnetized material

3)The case including magnetized material(vector potential Eq.)

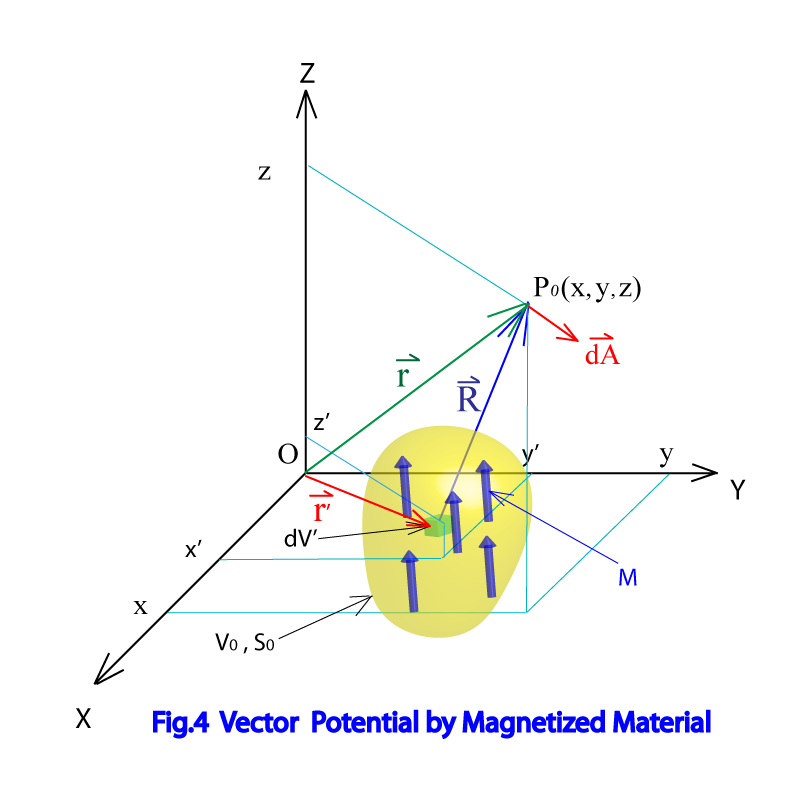
Next we consider the Eq. in the case including magnetized material. As shown in Fig.4 , magnetized material is in the area of $V_{0}$ , and also surface area is defined by $S_{0}$ in this volume magnetic dipole moment $\overset{⃑}{m_{i}}$ are included. We call the magnetic dipole moment included in the small area dV’

$\overset{⃑}{M} = \frac{1}{d V} \sum_{i} \overset{⃑}{m_{i}}$ Eq. (1-25)

as magnetization.

In section2, we found vector potential made by magnetic dipole moment could be delived as Eq. (1-7). So the vector potentil made by magnetic material at pont P0 showed in Fig.4 is expressed as

$\overset{⃑}{A} (x, y, z) = \frac{μ_{0}}{4 π} ∭_{V_{0}}^{} \frac{1}{R^{3}} \overset{⃑}{M} \times \overset{⃑}{R} d V'$ Eq. (1-26)

And from Fig.4, we can confirm as below Eq.(1-27).

$\begin{matrix} \overset{⃑}{R} = \overset{⃑}{r} - {\overset{⃑}{r}}^{'} = (x - x^{'}, y - y^{'}, z - z') \\ R = \sqrt{{(x - x^{'})}^{2} + {(y - y^{'})}^{2} + {(z - z^{'})}^{2}} \end{matrix}\}$ Eq. (1-27)

磁性体によるベクトルポテンシャル

$\overset{⃑}{\nabla} \frac{1}{R} = \frac{\partial}{\partial x} \frac{1}{\sqrt{{(x - x^{'})}^{2} + {(y - y^{'})}^{2} + {(z - z^{'})}^{2}}} \overset{⃑}{e_{x}} + \frac{\partial}{\partial y} \frac{1}{\sqrt{{(x - x^{'})}^{2} + {(y - y^{'})}^{2} + {(z - z^{'})}^{2}}} \overset{⃑}{e_{y}} + \frac{\partial}{\partial z} \frac{1}{\sqrt{{(x - x^{'})}^{2} + {(y - y^{'})}^{2} + {(z - z^{'})}^{2}}} \overset{⃑}{e_{z}}$

$= - \frac{x - x'}{{\sqrt{{(x - x^{'})}^{2} + {(y - y^{'})}^{2} + {(z - z^{'})}^{2}}}^{3}} \overset{⃑}{e_{x}} - \frac{y - y'}{{\sqrt{{(x - x^{'})}^{2} + {(y - y^{'})}^{2} + {(z - z^{'})}^{2}}}^{3}} \overset{⃑}{e_{y}} - \frac{z - z'}{{\sqrt{{(x - x^{'})}^{2} + {(y - y^{'})}^{2} + {(z - z^{'})}^{2}}}^{3}} \overset{⃑}{e_{z}}$

$= - \frac{\overset{⃑}{R}}{R^{3}}$ Eq. (1-28)

Here in the Eq. (1-28) we can replace $\overset{⃑}{\nabla}$ as ${\overset{⃑}{\nabla}}^{'} = \frac{\partial}{\partial x'} \overset{⃑}{e_{x}} + \frac{\partial}{\partial y'} \overset{⃑}{e_{x}} + \frac{\partial}{\partial z'} \overset{⃑}{e_{x}}$ . So Eq. (1-28) can expressed as below.

$\overset{⃑}{\nabla}' \frac{1}{R} = \frac{\partial}{\partial x'} \frac{1}{\sqrt{{(x - x^{'})}^{2} + {(y - y^{'})}^{2} + {(z - z^{'})}^{2}}} \overset{⃑}{e_{x}} + \frac{\partial}{\partial y'} \frac{1}{\sqrt{{(x - x^{'})}^{2} + {(y - y^{'})}^{2} + {(z - z^{'})}^{2}}} \overset{⃑}{e_{y}} + \frac{\partial}{\partial z'} \frac{1}{\sqrt{{(x - x^{'})}^{2} + {(y - y^{'})}^{2} + {(z - z^{'})}^{2}}} \overset{⃑}{e_{z}}$

$= - \frac{- (x - x')}{{\sqrt{{(x - x^{'})}^{2} + {(y - y^{'})}^{2} + {(z - z^{'})}^{2}}}^{3}} \overset{⃑}{e_{x}} - \frac{- (y - y')}{{\sqrt{{(x - x^{'})}^{2} + {(y - y^{'})}^{2} + {(z - z^{'})}^{2}}}^{3}} \overset{⃑}{e_{y}} - \frac{- (z - z')}{{\sqrt{{(x - x^{'})}^{2} + {(y - y^{'})}^{2} + {(z - z^{'})}^{2}}}^{3}} \overset{⃑}{e_{z}}$

$= - \overset{⃑}{\nabla} \frac{1}{R}$ Eq. (1-29)

So the Eq. Eq. (1-26) can express as below Eq.(1-30).

$\overset{⃑}{A} (x, y, z) = \frac{μ_{0}}{4 π} ∭_{V_{0}}^{} \overset{⃑}{M} \times (\overset{⃑}{\nabla}' \frac{1}{R}) d V'$ Eq. (1-30)

Next we use below vector caluculation formula below.

$\begin{matrix} \overset{⃑}{\nabla} φ \times \overset{⃑}{F} = \overset{⃑}{\nabla} \times (φ \overset{⃑}{F}) - φ (\overset{⃑}{\nabla} \times \overset{⃑}{F}) \\ ∭_{V_{0}}^{} \overset{⃑}{\nabla} \times \overset{⃑}{F} d V = - \iint_{S_{0}}^{} \overset{⃑}{F} \times \overset{⃑}{n} d A \end{matrix}\}$ Eq. (1-31)

（ $\overset{⃑}{n}$ は　stand for unit normal vector of the small area dA on the surface S0 in the volume $V_{0)}$ And the integral in the Eq. (1-30) can be replaced using upper side equation in Eq.(1-31) as,

$\overset{⃑}{M} \times (\overset{⃑}{\nabla}' \frac{1}{R}) = - (\overset{⃑}{\nabla}' \frac{1}{R}) \times \overset{⃑}{M} = - \{\overset{⃑}{\nabla}' \times (\frac{1}{R} \overset{⃑}{M}) - \frac{1}{R} (\overset{⃑}{\nabla}' \times \overset{⃑}{M})\}$ Eq. (1-32)

So the Eq. (1-30) can be written as below.

$\overset{⃑}{A} (x, y, z) = - \frac{μ_{0}}{4 π} ∭_{V_{0}}^{} {\overset{⃑}{\nabla}}^{'} \times (\frac{1}{R} \overset{⃑}{M}) {d V}^{'} + \frac{μ_{0}}{4 π} ∭_{V_{0}}^{} \frac{1}{R} (\overset{⃑}{\nabla}' \times \overset{⃑}{M}) d V'$ Eq. (1-33)

In above Eq. if using lower side equation in Eq.(1-31) we can get

$\overset{⃑}{A} (x, y, z) = \frac{μ_{0}}{4 π} \iint_{S_{0}}^{} \frac{1}{R} \overset{⃑}{M} \times \overset{⃑}{n} {d A}^{'} + \frac{μ_{0}}{4 π} ∭_{V_{0}}^{} \frac{1}{R} (\overset{⃑}{\nabla}' \times \overset{⃑}{M}) d V'$ Eq. (1-34)

Here we define equivarent electric density of magnetization M in the V_0 as,

$\overset{⃑}{J_{M}} = \overset{⃑}{\nabla}' \times M$ Eq. (1-35)

Also define the equivarent electric density of magnetization on the surface S_0 as,　

$\overset{⃑}{j_{M}} = \overset{⃑}{M} \times \overset{⃑}{n}$ Eq. (1-36)

Then we can express Eq. (1-34) as below.

$\overset{⃑}{A} (x, y, z) = \frac{μ_{0}}{4 π} \iint_{S_{0}}^{} \frac{1}{R} \overset{⃑}{j_{M}} {d A}^{'} + \frac{μ_{0}}{4 π} ∭_{V_{0}}^{} \frac{1}{R} \overset{⃑}{J_{M}} d V'$ Eq. (1-37)

Then if we caluculate rotation directly from above Eq.(1-37) , can get magnetiz field , howewver vector potential is vector value so equations will become complicated. So in the next section we will delive magnetic field from directly from Eq. (1-26).

Publication Date：16May2015 　　　　updated：27Jan2018
Author：Nobuo Kojima
Mail To：
2011-2020 Copyright by Kojimag