§１１．円柱曲線ワイヤーに流れる電流により作られる磁界 1)磁界の表式

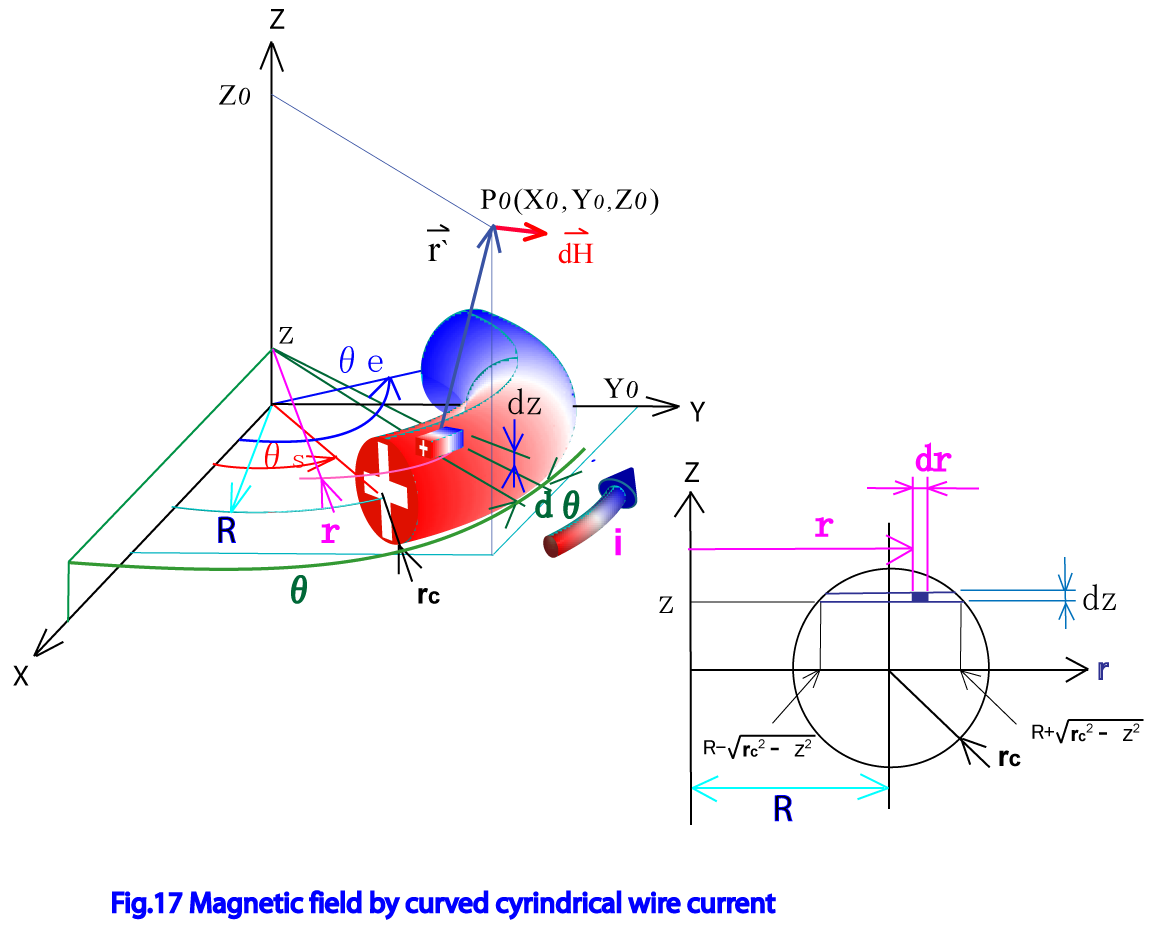
§１１．円柱曲線ワイヤーに流れる電流により作られる磁界

1)磁界の表式

円柱曲線ワイヤーに流れる電流により作られる磁界

Fig.11に示したように一定の曲率Rの円柱曲線型の電流要素を定義する。この電流要素を定義する固有座標系X-Y-Z は、原点が半径Rの円弧の中心とし、円弧はZ=0 のX-Y平面上にあるとする。また半径Rの円弧に沿って、開始角度 θ_s から終了角度θ_e までの範囲に半径 r_c の太さの導線が円弧Rを中心として存在するとする。また電流は電流密度iでFig.8　に示したように導線の内部に円周方向に沿って流れているとする。この時導線内の微小要素を考える。この微小要素はFig.8 に示したように円筒座標系（r、θ、Z）で（dr、dθ、dZ）の微小広がりで定義されているものとする。固有座標系X-Y-Zの点 $Ｐ_{0} (Ｘ_{０}, Ｙ_{０}, Ｚ_{０})$ に作られる磁界を表式化する。微小要素に流れる電流はi dr dz であり電流が流れる方向の長さはr dθ　であるのでこの微小電流要素が点 $P_{0}$ に作る磁界はビオサバールの法則により

$\overset{⃑}{d H} = \frac{1}{4 π} \frac{i ∙ d r ∙ d z ∙ (r d θ {\overset{⃑}{e}}_{θ}) \times \overset{⃑}{r'}}{{r'}^{3}}$ 式(11-1)

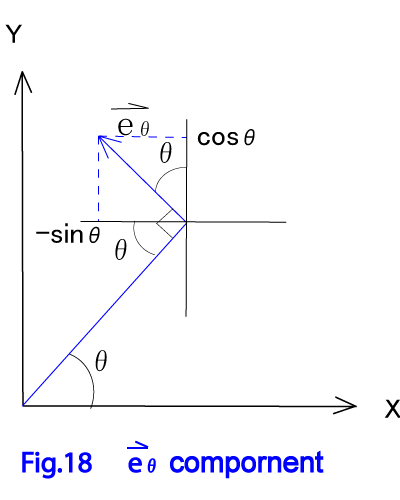
と表す事ができる。ここで ${\overset{⃑}{e}}_{θ}$ はθ方向の単位ベクトルで

${\overset{⃑}{e}}_{θ} = (- \sin θ, \cos θ, 0)$ 式(11-2)

である。(Fig.8-1参照)微小要素の位置は固有座標系で $(r \cos θ, r \sin θ, Z)$ であり $\overset{⃑}{r'}$ は

$\overset{⃑}{r'} ＝ (X_{0} - r \cos θ, Y_{0} - r \sin θ, Z_{0} - Z)$ 式(11-3)

と表せるので、式(11-1)の外積　 ${\overset{⃑}{e}}_{θ} \times \overset{⃑}{r'}$ 　は

${\overset{⃑}{e}}_{θ} \times \overset{⃑}{r'} ＝ (\cos θ (Z_{0} - z), \sin θ (Z_{0} - z),$

$- \sin θ (Y_{0} - r ∙ \sin θ) - \cos θ (X_{0} - r ∙ \cos θ))$

となる。

従って式(11-1)は

$\begin{matrix} {d H}_{x} = \frac{1}{4 π} \frac{1}{{r^{'}}^{3}} i r d r d θ d z \cos θ (Z_{0} - z) \\ {d H}_{y} = \frac{1}{4 π} \frac{1}{{r'}^{3}} i r d r d θ d z \sin θ (Z_{0} - z) \\ {d H}_{z} = \frac{1}{4 π} \frac{1}{{r'}^{3}} i r d r d θ d z [- \sin θ (Y_{0} - r ∙ \sin θ) - \cos θ (X_{0} - r ∙ \cos θ)] \end{matrix}\}$ 式(11-4)

ここで

$r' = \sqrt{{(X_{0} - r ∙ \cos θ)}^{2} + {(Y_{0} - r ∙ \sin θ)}^{2} + {(Z_{0} - z)}^{2}}$ 式(11-5)

と表せる。Hx　,Hy,　Hz　は式(11-4)をr,　 θ,　z　に関してコイルの全範囲に渡って積分する事によって求める事ができ

$\begin{matrix} H_{x} = \frac{i}{4 π} \int_{R - \sqrt{{r_{c}}^{2} - z^{2}}}^{R + \sqrt{{r_{c}}^{2} - z^{2}}} r d r \int_{θ_{s}}^{θ_{e}} \cos θ d θ \int_{- r_{c}}^{r_{c}} \frac{Z_{0} - z}{{\sqrt{{(X_{0} - r ∙ \cos θ)}^{2} + {(Y_{0} - r ∙ \sin θ)}^{2} + {(Z_{0} - z)}^{2}}}^{3}} d z \\ H_{y} = \frac{i}{4 π} \int_{R - \sqrt{{r_{c}}^{2} - z^{2}}}^{R + \sqrt{{r_{c}}^{2} - z^{2}}} r d r \int_{θ_{s}}^{θ_{e}} \sin θ \int_{- r_{c}}^{r_{c}} \frac{Z_{0} - z}{{\sqrt{{(X_{0} - r ∙ \cos θ)}^{2} + {(Y_{0} - r ∙ \sin θ)}^{2} + {(Z_{0} - z)}^{2}}}^{3}} d z \\ H_{z} = \frac{i}{4 π} \int_{R - \sqrt{{r_{c}}^{2} - z^{2}}}^{R + \sqrt{{r_{c}}^{2} - z^{2}}} r d r \int_{θ_{s}}^{θ_{e}} d θ \int_{- r_{c}}^{r_{c}} \frac{- \sin θ (Y_{0} - r ∙ \sin θ) - \cos θ (X_{0} - r ∙ \cos θ)}{{\sqrt{{(X_{0} - r ∙ \cos θ)}^{2} + {(Y_{0} - r ∙ \sin θ)}^{2} + {(Z_{0} - z)}^{2}}}^{3}} d z \end{matrix}\}$ 式(11-6)

と表せる。式(11-5)をrに関して展開すると

$r' = \sqrt{r^{2} - 2 (X_{0} \cos θ + Y_{0} \sin θ) {r + {X_{0}}^{2} + {Y_{0}}^{2} + (Z_{0} - z)}^{2}}$

$= \sqrt{{\{r - (X_{0} \cos θ + Y_{0} \sin θ)\}}^{2} {- {(X_{0} \cos θ + Y_{0} \sin θ)}^{2} + {X_{0}}^{2} + {Y_{0}}^{2} + (Z_{0} - z)}^{2}}$

$= \sqrt{{\{r - (X_{0} \cos θ + Y_{0} \sin θ)\}}^{2} {+ {(X_{0} \sin θ - Y_{0} \cos θ)}^{2} + (Z_{0} - z)}^{2}}$ 式(11-7)

ここで

$t = r - (X_{0} \cos θ + Y_{0} \sin θ)$

$C = {{(X_{0} \sin θ - Y_{0} \cos θ)}^{2} + (Z_{0} - z)}^{2}$

とおくと式(11-7)は

$r^{'} = \sqrt{t^{2} + C}$ 式(11-8)

と書ける。従って式(11-6)のrに関する積分をtに関する積分に置き換えると

$\begin{matrix} H_{x} = \frac{i}{4 π} \int_{θ_{s}}^{θ_{e}} \cos θ d θ \int_{- r_{c}}^{r_{c}} (Z_{0} - z) d z \int_{R_{z -}}^{R_{z +}} \frac{t + (X_{0} \cos θ + Y_{0} \sin θ)}{{\sqrt{t^{2} + C}}^{3}} d t \\ H_{y} = \frac{i}{4 π} \int_{θ_{s}}^{θ_{e}} \sin θ d θ \int_{- r_{c}}^{r_{c}} (Z_{0} - z) d z \int_{R_{z -}}^{R_{z +}} \frac{t + (X_{0} \cos θ + Y_{0} \sin θ)}{{\sqrt{t^{2} + C}}^{3}} d t \\ H_{z} = \frac{i}{4 π} \int_{θ_{s}}^{θ_{e}} d θ \int_{- r_{c}}^{r_{c}} d z \int_{R_{z -}}^{R_{z +}} \frac{t + (X_{0} \cos θ + Y_{0} \sin θ)}{{\sqrt{t^{2} + C}}^{3}} \\ ∙ [- \sin θ (Y_{0} - \{t + (X_{0} \cos θ + Y_{0} \sin θ)\} \sin θ) - \cos θ (X_{0} - \{t + (X_{0} \cos θ + Y_{0} \sin θ)\} \cos θ)] d t \end{matrix}\}$ 式(11-8)

ここで

$\begin{matrix} R_{z +} ＝ R + \sqrt{{r_{c}}^{2} - z^{2}} - (X_{0} \cos θ + Y_{0} \sin θ) \\ R_{z -} ＝ R - \sqrt{{r_{c}}^{2} - z^{2}} - (X_{0} \cos θ + Y_{0} \sin θ) \end{matrix}\}$ 式(11-9)

とおいた。

　先ず式(11-8) において tに関する積分を行う。その時、数学公式Ⅰ（岩波全書）の以下の不定積分公式を利用する。o

$\int \frac{d x}{{(a x^{2} + b x + c)}^{3 / 2}} = \frac{2 (2 a x + b)}{(4 a c - b^{2}) \sqrt{a x^{2} + b x + c}}$ 式(11-10)

$\int \frac{x d x}{{(a x^{2} + b x + c)}^{3 / 2}} = \frac{2 (b x + 2 c)}{(b^{2} - 4 a c) \sqrt{a x^{2} + b x + c}}$ 式(11-11)

$\int \frac{x^{2} d x}{{(a x^{2} + b x + c)}^{3 / 2}} = \frac{({2 b}^{2} - 4 a c) x + 2 b c}{a (4 a c {- b}^{2}) \sqrt{a x^{2} + b x + c}}$

$+ \frac{1}{a^{3 / 2}} l o g |2 a x + b + 2 \sqrt{a (a x^{2} + b x + c)}|$ 　　　　　a>0の時式(11-12)

　a=1 , b=0　とすると上の公式は

$\int \frac{d x}{{(x^{2} + c)}^{3 / 2}} = \frac{x}{c \sqrt{x^{2} + c}}$ 式(11-10')

$\int \frac{x d x}{{(x^{2} + c)}^{3 / 2}} = \frac{- 1}{\sqrt{x^{2} + c}}$ 式(11-11')

$\int \frac{x^{2} d x}{{(x^{2} + c)}^{3 / 2}} = \frac{- x}{\sqrt{x^{2} + c}} + l o g |2 x + 2 \sqrt{x^{2} + c}|$ 式(11-12')

となる。

--------磁石専用磁場計算アプリケーション(Kojimag)に興味がある方はこちらへ--------

このサイトの基礎計算式を基に磁石専用アプリケーションを開発しました。
こちらから”磁石専用磁場計算アプリケーション(Kojimag)”からKojimagの詳細について確認できます。