§１４．一般角柱磁石により作られる磁界２）各磁極面の磁化からの磁場への寄与

§１４．一般角柱磁石により作られる磁界

２）各磁極面の磁化からの磁場への寄与

1) 上面からの磁場への寄与

これは既に§３において表式化した。 Hx ,　Hy,　Hzが夫々、式(3-11),　式(3-12),　式(3-15)　に示される。ここで、Br の代わりに、M cos⁡θ を代入するものとする。

2) 右側面からの寄与

Fig.14-2に右側面の座標系 $(X_{R}, Y_{R}, Z_{R})$ 　を示す。

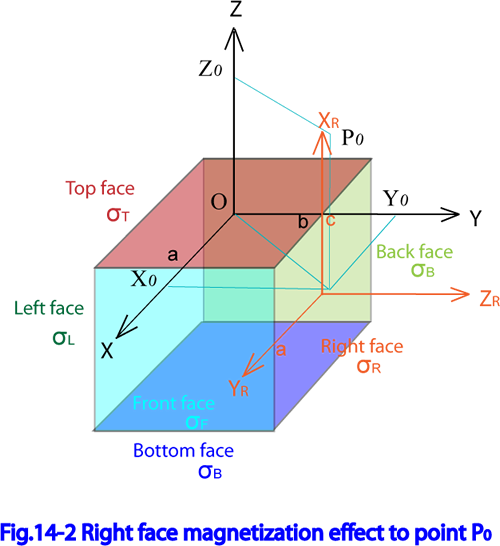
右側面磁化からの寄与

ここで、固有座標系　 $(X, Y, Z)$ と右側面座標系 ${(X}_{R}, Y_{R}, Z_{R})$ との関係は

$X_{R} = Z + c, Y_{R} = X, Z_{R} = Y - b$ 式(14-2)

となる。従って点 $P_{0} (X_{0}, Y_{0}, Z_{0})$ は、 $X_{R}, Y_{R}, Z_{R}$ 　座標系で $(Z_{0} + c, X_{0}, Y_{0} - b)$ になる。右側面の表面磁化 $σ_{R}$ が点　 $P_{0} (X_{0}, Y_{0}, Z_{0})$ 　に作る磁界のX成分は $X_{R}, Y_{R}, Z_{R}$ 座標系の $Y_{R}$ 成分となるので、§３の式(3-12)　で表される。ただし、磁極面は、 $(a, b)$ の代わりに $(c, a)$ となる。また点　 $P_{0} (X_{0}, Y_{0}, Z_{0})$ 　の代わりに $P_{0} (Z_{0} + c, X_{0}, Y_{0} - b)$ となる。従って

$H_{XR} = \frac{σ_{R}}{4 π μ_{0}} \log (\frac{(Z_{0} + 2 c) + \sqrt{{(Z_{0} + 2 c)}^{2} + {(X_{0} - a)}^{2} + {(Y_{0} - b)}^{2}}}{(Z_{0} + 2 c) + \sqrt{{{(Z_{0} + 2 c)}^{2} + (X_{0} + a)}^{2} + {(Y_{0} - b)}^{2}}} \frac{Z_{0} + \sqrt{{{Z_{0}}^{2} + (X_{0} + a)}^{2} + {(Y_{0} - b)}^{2}}}{Z_{0} + \sqrt{{{Z_{0}}^{2} + (X_{0} - a)}^{2} + {(Y_{0} - b)}^{2}}})$ 式(14-3)

と表せる。次に磁界のY成分は、 $X_{R}, Y_{R}, Z_{R}$ 座標系の $Z_{R}$ 成分となるので、§３の式(3-15) で表される。同様に磁極面は、 $(a, b)$ の代わりに $(c, a)$ 、また点　 $P_{0} (X_{0}, Y_{0}, Z_{0})$ 　　の代わりに　 $P_{0} (Z_{0} + c, X_{0}, Y_{0} - b)$ 　となる。従って

$H_{YR} = \frac{σ_{R}}{4 π μ_{0}} \{\tan^{- 1} (\frac{1}{Z_{0}} \frac{(Z_{0} + 2 c) (X_{0} + a)}{\sqrt{{(Z_{0} + 2 c)}^{2} + {(X_{0} + a)}^{2} + {(Y_{0} - b)}^{2}}}) - \tan^{- 1} (\frac{1}{Z_{0}} \frac{(Z_{0} + 2 c) (X_{0} - a)}{\sqrt{{(Z_{0} + 2 c)}^{2} + {(X_{0} - a)}^{2} + {(Y_{0} - b)}^{2}}})\}$

$- \frac{σ_{R}}{4 π μ_{0}} \{\tan^{- 1} (\frac{1}{Z_{0}} \frac{Z_{0} (X_{0} + a)}{\sqrt{{Z_{0}}^{2} + {(X_{0} + a)}^{2} + {(Y_{0} - b)}^{2}}}) - \tan^{- 1} (\frac{1}{Z_{0}} \frac{Z_{0} (X_{0} - a)}{\sqrt{{Z_{0}}^{2} + {(X_{0} - a)}^{2} + {(Y_{0} - b)}^{2}}})\}$ 式(14-4)

次に磁界のZ成分は、 $X_{R}, Y_{R}, Z_{R}$ 座標系の $X_{R}$ 成分となるので、§３の式(3-11) で表される。同様に磁極面は、 $(a, b)$ の代わりに $(c, a)$ 、また点　 $P_{0} (X_{0}, Y_{0}, Z_{0})$ 　　の代わりに　 $P_{0} (Z_{0} + c, X_{0}, Y_{0} - b)$ 　となる。従って

$H_{ZR} = \frac{σ_{R}}{4 π μ_{0}} \log (\frac{(X_{0} + a) + \sqrt{{Z_{0}}^{2} + {(X_{0} + a)}^{2} + {(Y_{0} - b)}^{2}}}{(X_{0} + a) + \sqrt{{{(Z_{0} + 2 c)}^{2} + (X_{0} + a)}^{2} + {(Y_{0} - b)}^{2}}} \frac{(X_{0} - a) + \sqrt{{(Z_{0} + 2 c)}^{2} + {(X_{0} - a)}^{2} + {(Y_{0} - b)}^{2}}}{(X_{0} - a) + \sqrt{{Z_{0}}^{2} + {(X_{0} - a)}^{2} + {(Y_{0} - b)}^{2}}})$ 式(14-5)

3) 前面からの寄与

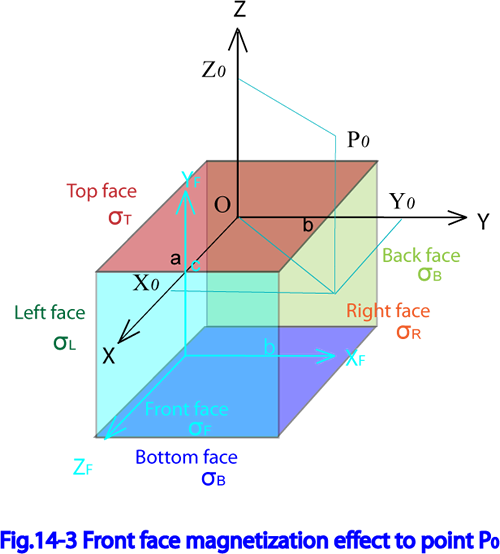
前面磁化からの寄与の図

Fig.14-3に前面の座標系　 $(X_{F}, Y_{F}, Z_{F})$ を示す。ここで、固有座標系　 $(X, Y, Z)$ と前面座標系 $(X_{F}, Y_{F}, Z_{F})$ との関係は

$X_{F} = Y, Y_{F} = Z + c, Z_{F} = X - a$ 式(14-6)

となる。
従って点 $P_{0} (X_{0}, Y_{0}, Z_{0})$ は、 $X_{R}, Y_{R}, Z_{R}$ 　座標系で $(Y_{0}, Z_{0} + c, X_{0} - a)$ になる。前面の表面磁化 $σ_{F}$ が点　 $P_{0} (X_{0}, Y_{0}, Z_{0})$ に作る磁界のX成分は $X_{F}, Y_{F}, Z_{F}$ 座標系の $Z_{F}$ 成分となるので、§３の式(3-15)　で表される。ただし、磁極面は、 $(a, b)$ の代わりに $(b, c)$ となる。また点　 $P_{0} (X_{0}, Y_{0}, Z_{0})$ の代わりに　 $P_{0} (Y_{0}, Z_{0} + c, X_{0} - a)$ 　となる。
従って

$H_{XF} = \frac{σ_{F}}{4π μ_{0}} \{{tan}^{-1} (\frac{1}{(X_{0} -a)} \frac{(Y_{0} +b) (Z_{0} +2c)}{\sqrt{{(Y_{0} +b)}^{2} + {(Y_{0} +c)}^{2} + {(X_{0} -a)}^{2}}}) - {tan}^{-1} (\frac{1}{(X_{0} -a)} \frac{(Y_{0} +b) Z_{0}}{\sqrt{{(Y_{0} +b)}^{2} + {(Y_{0} -c)}^{2} + {(X_{0} -a)}^{2}}})\}$

$- \frac{σ_{F}}{4π μ_{0}} \{{tan}^{-1} (\frac{1}{(X_{0} -a)} \frac{(Y_{0} - b) (Z_{0} +2c)}{\sqrt{{(Y_{0} -b)}^{2} + {(Z_{0} +2c)}^{2} + {(X_{0} -a)}^{2}}}) - {tan}^{-1} (\frac{1}{(X_{0} -a)} \frac{(Y_{0} -b) Z_{0}}{\sqrt{{(Y_{0} -b)}^{2} + {Z_{0}}^{2} + {(X_{0} -a)}^{2}}})\}$ 式(14-7)

次に磁界のY成分は、 $X_{F}, Y_{F}, Z_{F}$ 座標系の $X_{F}$ 成分となるので、§３の式(3-11) で表される。同様に磁極面は、 $(a, b)$ の代わりに $(b, c)$ 、また点　 $P_{0} (X_{0}, Y_{0}, Z_{0})$ 　　の代わりに　 $P_{0} (Y_{0}, Z_{0} + c, X_{0} - a)$ 　となる。
従って

$H_{YF} = \frac{σ_{F}}{4 π μ_{0}} \log (\frac{Z_{0} +2c + \sqrt{{(Y_{0} -b)}^{2} + {(Z_{0} +2c)}^{2} + {(X_{0} -a)}^{2}}}{Z_{0} +2c + \sqrt{{{(Y_{0} +b)}^{2} + (Z_{0} +2c)}^{2} + {(X_{0} -a)}^{2}}} \frac{Z_{0} + \sqrt{{(Y_{0} +b)}^{2} + {Z_{0}}^{2} + {(X_{0} -a)}^{2}}}{Z_{0} + \sqrt{{(Y_{0} -b)}^{2} + {Z_{0}}^{2} + {(X_{0} -a)}^{2}}})$ 式(14-8)

次に磁界のZ成分は、 $X_{F}, Y_{F}, Z_{F}$ 座標系の $Y_{F}$ 成分となるので、§３の式(3-12) で表される。同様に磁極面は、 $(a, b)$ の代わりに $(b, c)$ 、また点　 $P_{0} (X_{0}, Y_{0}, Z_{0})$ 　　の代わりに　 $P_{0} (Y_{0}, Z_{0} + c, X_{0} - a)$ 　となる。
従って

$H_{ZF} = \frac{σ_{F}}{4 π μ_{0}} \log (\frac{(Y_{0} + b) + \sqrt{{(Y_{0} + b)}^{2} + {Z_{0}}^{2} + {(X_{0} - a)}^{2}}}{(Y_{0} + b) + \sqrt{{{(Y_{0} + b)}^{2} + (Z_{0} + 2 c)}^{2} + {(X_{0} - a)}^{2}}} \frac{(Y_{0} - b) + \sqrt{{{(Y_{0} - b)}^{2} + (Z_{0} + 2 c)}^{2} + {(X_{0} - a)}^{2}}}{(Y_{0} - b) + \sqrt{{(Y_{0} - b)}^{2} + Z_{0}^{2} + {(X_{0} - a)}^{2}}})$ 式(14-9)

4) 左側面からの寄与

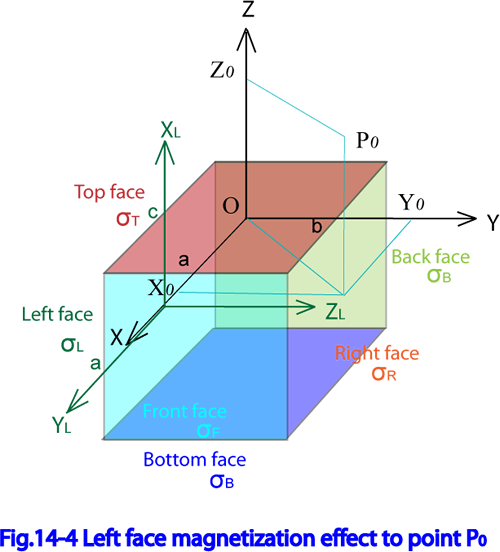
左側面磁化からの寄与の図

Fig.14-4に左側面の座標系　 $(X_{L}, Y_{L}, Z_{L})$ を示す。ここで、固有座標系　 $(X, Y, Z)$ と右側面座標系 $(X_{L}, Y_{L}, Z_{L})$ との関係は

$X_{L} = Z + c, Y_{L} = X, Z_{L} = Y + b$ 式(14-10)

となる。従って点 $P_{0} (X_{0}, Y_{0}, Z_{0})$ は、 $X_{L}, Y_{L}, Z_{L}$ 　座標系で $(Z_{0} + c, X_{0}, Y_{0} + b)$ になる。右側面の表面磁化 $σ_{L}$ が点　 $P_{0} (X_{0}, Y_{0}, Z_{0})$ 　に作る磁界のX成分は $X_{L}, Y_{L}, Z_{L}$ 座標系の $Y_{L}$ 成分となるので、§３の式(3-12)　で表される。ただし、磁極面は、 $(a, b)$ の代わりに $(c, a)$ となる。また点　 $P_{0} (X_{0}, Y_{0}, Z_{0})$ の代わりに $P_{0} (Z_{0} + c, X_{0}, Y_{0} + b)$ 　となる。
従って

$H_{X L} = \frac{σ_{L}}{4 π μ_{0}} \log (\frac{(Z_{0} + 2 c) + \sqrt{{(Z_{0} + 2 c)}^{2} + {(X_{0} - a)}^{2} + {(Y_{0} + b)}^{2}}}{(Z_{0} + 2 c) + \sqrt{{{(Z_{0} + 2 c)}^{2} + (X_{0} + a)}^{2} + {(Y_{0} + b)}^{2}}} \frac{Z_{0} + \sqrt{{{Z_{0}}^{2} + (X_{0} + a)}^{2} + {(Y_{0} + b)}^{2}}}{Z_{0} + \sqrt{{{Z_{0}}^{2} + (X_{0} - a)}^{2} + {(Y_{0} + b)}^{2}}})$ 式(14-11)

次に磁界のY成分は、 $X_{L}, Y_{L}, Z_{L}$ 座標系の $Z_{L}$ 成分となるので、§３の式(3-15) で表される。同様に磁極面は、 $(a, b)$ 　の代わりに $(c, a)$ 、また点　 $P_{0} (X_{0}, Y_{0}, Z_{0})$ 　の代わりに　 $P_{0} (Z_{0} + c, X_{0}, Y_{0} + b)$ 　となる。
従って

$H_{Y L} = \frac{σ_{L}}{4 π μ_{0}} \{\tan^{- 1} (\frac{1}{(Y_{0} + b)} \frac{(Z_{0} + 2 c) (X_{0} + a)}{\sqrt{{(Z_{0} + 2 c)}^{2} + {(X_{0} + a)}^{2} + {(Y_{0} + b)}^{2}}}) - \tan^{- 1} (\frac{1}{(Y_{0} + b)} \frac{(Z_{0} + 2 c) (X_{0} - a)}{\sqrt{{(Z_{0} + 2 c)}^{2} + {(X_{0} - a)}^{2} + {(Y_{0} + b)}^{2}}})\}$

$- \frac{σ_{L}}{4 π μ_{0}} \{\tan^{- 1} (\frac{1}{(Y_{0} + b)} \frac{Z_{0} (X_{0} + a)}{\sqrt{{Z_{0}}^{2} + {(X_{0} + a)}^{2} + {(Y_{0} + b)}^{2}}}) - \tan^{- 1} (\frac{1}{(Y_{0} + b)} \frac{Z_{0} (X_{0} - a)}{\sqrt{{Z_{0}}^{2} + {(X_{0} - a)}^{2} + {(Y_{0} + b)}^{2}}})\}$ 式(14-12)

次に磁界のZ成分は、 $X_{L}, Y_{L}, Z_{L}$ 座標系の $X_{L}$ 成分となるので、§３の式(3-11) で表される。同様に磁極面は、 $(a, b)$ の代わりに $(c, a)$ 、また点　 $P_{0} (X_{0}, Y_{0}, Z_{0})$ 　の代わりに　 $P_{0} (Z_{0} + c, X_{0}, Y_{0} + b)$ 　となる。
従って

$H_{Z L} = \frac{σ_{L}}{4 π μ_{0}} \log (\frac{(X_{0} + a) + \sqrt{{Z_{0}}^{2} + {(X_{0} + a)}^{2} + {(Y_{0} + b)}^{2}}}{(X_{0} + a) + \sqrt{{{(Z_{0} + 2 c)}^{2} + (X_{0} + a)}^{2} + {(Y_{0} + b)}^{2}}} \frac{(X_{0} - a) + \sqrt{{(Z_{0} + 2 c)}^{2} + {(X_{0} - a)}^{2} + {(Y_{0} + b)}^{2}}}{(X_{0} - a) + \sqrt{{Z_{0}}^{2} + {(X_{0} - a)}^{2} + {(Y_{0} + b)}^{2}}})$ 式(14-13)

5) 背面からの寄与

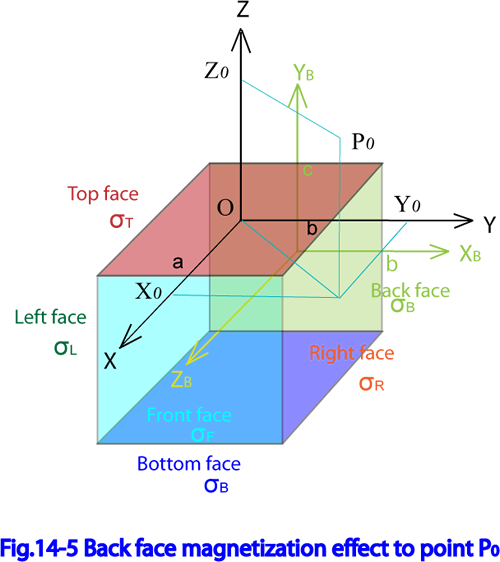
背面磁化からの寄与の図

Fig.14-5に背面の座標系　 ${(X}_{B}, Y_{B}, Z_{B})$ を示す。ここで、固有座標系　 $(X, Y, Z)$ と背面座標系 ${(X}_{B}, Y_{B}, Z_{B})$ との関係は

$X_{B} = Y, Y_{B} = Z + c, Z_{B} = X + a$ 式(14-14)

となる。従って $P_{0} (X_{0}, Y_{0}, Z_{0})$ は、 $X_{B}, Y_{B}, Z_{B}$ 　座標系で $(Y_{0}, Z_{0} + c, X_{0} + a)$ になる。背面の表面磁化 $σ_{B}$ が点　 $P_{0} (X_{0}, Y_{0}, Z_{0})$ に作る磁界のX成分は $X_{B}, Y_{B}, Z_{B}$ 座標系の $Z_{B}$ 成分となるので、§３の式(3-15)　で表される。ただし、磁極面は、 $(a, b)$ の代わりに $(b, c)$ となる。また点　 $P_{0} (X_{0}, Y_{0}, Z_{0})$ の代わりに　 $P_{0} (Y_{0}, Z_{0} + c, X_{0} + a)$ 　となる。
従って

$H_{XB} = \frac{σ_{B}}{4 π μ_{0}} \{\tan^{- 1} (\frac{1}{(X_{0} + a)} \frac{(Y_{0} + b) (Z_{0} + 2 c)}{\sqrt{{(Y_{0} + b)}^{2} + {(Z_{0} + 2 c)}^{2} + {(X_{0} + a)}^{2}}}) - \tan^{- 1} (\frac{1}{(X_{0} + a)} \frac{(Y_{0} + b) Z_{0}}{\sqrt{{(Y_{0} + b)}^{2} + {Z_{0}}^{2} + {(X_{0} + a)}^{2}}})\}$

$- \frac{σ_{B}}{4 π μ_{0}} \{\tan^{- 1} (\frac{1}{(X_{0} + a)} \frac{(Y_{0} - b) (Z_{0} + 2 c)}{\sqrt{{(Y_{0} - b)}^{2} + {(Z_{0} + 2 c)}^{2} + {(X_{0} + a)}^{2}}}) - \tan^{- 1} (\frac{1}{(X_{0} + a)} \frac{(Y_{0} - b) Z_{0}}{\sqrt{{(Y_{0} - b)}^{2} + {Z_{0}}^{2} + {(X_{0} + a)}^{2}}})\}$ 式(14-15)

次に磁界のY成分は、 $X_{B}, Y_{B}, Z_{B}$ 座標系の $X_{B}$ 成分となるので、§３の式(3-11) で表される。同様に磁極面は、 $(a, b)$ の代わりに $(b, c)$ 、また点　 $P_{0} (X_{0}, Y_{0}, Z_{0})$ 　　の代わりに　 $P_{0} (Y_{0}, Z_{0} + c, X_{0} + a)$ 　となる。
従って

$H_{YB} = \frac{σ_{B}}{4 π μ_{0}} \log (\frac{(Z_{0} + 2 c) + \sqrt{{(Y_{0} - b)}^{2} + {(Z_{0} + 2 c)}^{2} + {(X_{0} + a)}^{2}}}{(Z_{0} + 2 c) + \sqrt{{{(Y_{0} + b)}^{2} + (Z_{0} + 2 c)}^{2} + {(X_{0} + a)}^{2}}} \frac{Z_{0} + \sqrt{{(Y_{0} + b)}^{2} + {Z_{0}}^{2} + {(X_{0} + a)}^{2}}}{Z_{0} + \sqrt{{(Y_{0} - b)}^{2} + {Z_{0}}^{2} + {(X_{0} + a)}^{2}}})$ 式(14-16)

次に磁界のZ成分は、 $X_{B}, Y_{B}, Z_{B}$ 座標系の $Y_{B}$ 成分となるので、§３の式(3-12) で表される。同様に磁極面は、 $(a, b)$ の代わりに $(b, c)$ 、また点　 $P_{0} (X_{0}, Y_{0}, Z_{0})$ 　　の代わりに　 $P_{0} (Y_{0}, Z_{0} + c, X_{0} + a)$ )　となる。従って

$H_{ZB} = \frac{σ_{B}}{4 π μ_{0}} \log (\frac{(Y_{0} + b) + \sqrt{{(Y_{0} + b)}^{2} + {Z_{0}}^{2} + {(X_{0} + a)}^{2}}}{(Y_{0} + b) + \sqrt{{{(Y_{0} + b)}^{2} + (Z_{0} + 2 c)}^{2} + {(X_{0} + a)}^{2}}} \frac{(Y_{0} - b) + \sqrt{{{(Y_{0} - b)}^{2} + (Z_{0} + 2 c)}^{2} + {(X_{0} + a)}^{2}}}{(Y_{0} - b) + \sqrt{{(Y_{0} - b)}^{2} + Z_{0}^{2} + {(X_{0} + a)}^{2}}})$ 式(14-17)

6) 底面からの寄与

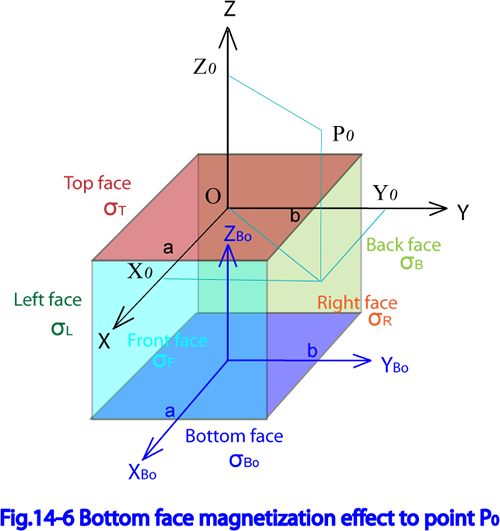
底面磁化からの寄与の図

Fig.14-6底面の座標系　 $(X_{B o}, Y_{B o}, Z_{B o})$ を示す。ここで、固有座標系　 $(X, Y, Z)$ と背面座標系 ${(X}_{B o}, Y_{B o}, Z_{B o})$ との関係は

$X_{B o} = X, Y_{B o} = Y, Z_{B o} = Z + 2 c$ 式(14-18)

となる。従って点 $P_{0} (X_{0}, Y_{0}, Z_{0})$ は、 $X_{B o}, Y_{B o}, Z_{B o}$ 　座標系で $(X_{0}, Y_{0}, Z_{0} + 2 c)$ になる。底面の表面磁化 $σ_{Bo}$ が点　 $P_{0} (X_{0}, Y_{0}, Z_{0})$ 　に作る磁界のX成分は $X_{B o}, Y_{B o}, Z_{B o}$ 座標系の $X_{Bo}$ 成分となるので、§３の式(3-11)　で表される。ただし、磁極面は、 $(a, b)$ のままである。また点　 $P_{0} (X_{0}, Y_{0}, Z_{0})$ 　の代わりに　 $P_{0} (X_{0}, Y_{0}, Z_{0} + 2 c)$ 　となる。
従って

$H_{X B o} = \frac{σ_{Bo}}{4 π μ_{0}} \log (\frac{(Y_{0} + b) + \sqrt{{(X_{0} - a)}^{2} + {(Y_{0} + b)}^{2} + {(Z_{0} + 2 c)}^{2}}}{(Y_{0} + b) + \sqrt{{{(X_{0} + a)}^{2} + (Y_{0} + b)}^{2} + {(Z_{0} + 2 c)}^{2}}} \frac{(Y_{0} - b) + \sqrt{{(X_{0} + a)}^{2} + {(Y_{0} - b)}^{2} + {(Z_{0} + 2 c)}^{2}}}{(Y_{0} - b) + \sqrt{{(X_{0} - a)}^{2} + {(Y_{0} - b)}^{2} + {(Z_{0} + 2 c)}^{2}}})$ 式(14-19)

同様に　Y　成分は

$H_{Y B o} = \frac{σ_{Bo}}{4 π μ_{0}} \log (\frac{(X_{0} + a) + \sqrt{{(X_{0} + a)}^{2} + {(Y_{0} - b)}^{2} + {(Z_{0} + 2 c)}^{2}}}{(X_{0} + a) + \sqrt{{{(X_{0} + a)}^{2} + (Y_{0} + b)}^{2} + {(Z_{0} + 2 c)}^{2}}} \frac{(X_{0} - a) + \sqrt{{{(X_{0} - a)}^{2} + (Y_{0} + b)}^{2} + {(Z_{0} + 2 c)}^{2}}}{(X_{0} - a) + \sqrt{{{(X_{0} - a)}^{2} + (Y_{0} - b)}^{2} + {(Z_{0} + 2 c)}^{2}}})$ 式(14-20)

同様に　Z　成分は

$H_{Z B o} = \frac{σ_{Bo}}{4 π μ_{0}} \{\tan^{- 1} (\frac{1}{(Z_{0} + 2 c)} \frac{(X_{0} + a) (Y_{0} + b)}{\sqrt{{(X_{0} + a)}^{2} + {(Y_{0} + b)}^{2} + {(Z_{0} + 2 c)}^{2}}}) - \tan^{- 1} (\frac{1}{(Z_{0} + 2 c)} \frac{(X_{0} + a) (Y_{0} - b)}{\sqrt{{(X_{0} + a)}^{2} + {(Y_{0} - b)}^{2} + {(Z_{0} + 2 c)}^{2}}})\}$

$- \frac{σ_{Bo}}{4 π μ_{0}} \{\tan^{- 1} (\frac{1}{(Z_{0} + 2 c)} \frac{(X_{0} - a) (Y_{0} + b)}{\sqrt{{(X_{0} - a)}^{2} + {(Y_{0} + b)}^{2} + {(Z_{0} + 2 c)}^{2}}}) - \tan^{- 1} (\frac{1}{(Z_{0} + 2 c)} \frac{(X_{0} - a) (Y_{0} - b)}{\sqrt{{(X_{0} - a)}^{2} + {(Y_{0} - b)}^{2} + {(Z_{0} + 2 c)}^{2}}})\}$ 式(14-21)

--------磁石専用磁場計算アプリケーション(Kojimag)に興味がある方はこちらへ--------

このサイトの基礎計算式を基に磁石専用アプリケーションを開発しました。
こちらから”磁石専用磁場計算アプリケーション(Kojimag)”からKojimagの詳細について確認できます。

公開日：2013年10月14日　　　　　更新日：2023年10月16日
作成者：児島　伸生
　連絡先：
2011-2023 Copyright by Kojimag