§1-2) 磁気双極子

§１．磁性体を含む系の磁場の表式

２）磁気双極子

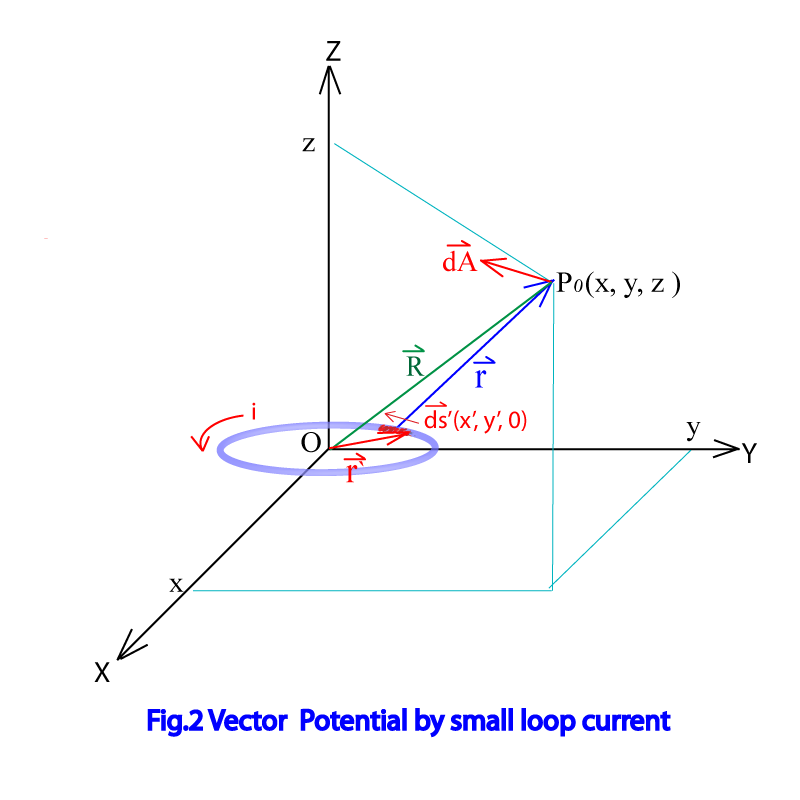
微小環電流によるベクトルポテンシャル

Fig.2に示した様な、小さい環を考え、環には一定電流ｉが流れているとする。環はxy平面上にあるとする。環上の位置 $\overset{⃑}{r'} (x', y', 0)$ にある微小ベクトル要素を $\overset{⃑}{d s'}$ とすると点 $P_{0} (x, y, z)$ のベクトルポテンシャルは

$\overset{⃑}{A} = \frac{μ_{0}}{4 π} ∭ \frac{\overset{⃑}{ｉ}}{r} d V' = \frac{μ_{0} ｉ}{4 π} \oint \frac{\overset{⃑}{d s}'}{r}$ 式(1-7)

ここで

$\overset{⃑}{r} = (x - x^{'}, y - y^{'}, z), r = \sqrt{{(x - x^{'})}^{2} + {(y - y^{'})}^{2} + z^{2}}$ 式(1-8)

また

$\overset{⃑}{R} = (x, y, z), R = \sqrt{x^{2} + y^{2} + z^{2}}$ 式(1-9)

である。環の大きさは点 $P_{0}$ 迄の距離に比べて十分に小さいと仮定し、 $R ≫ x^{'}, R ≫ y'$

と考え r を 1/R で展開し、 $x^{'}, y^{'}$ に関して1次の項までで近似する。式(1-8)は

$R = {[(x^{2} + y^{2} + z^{2}) \{1 - 2 (\frac{{x x}^{'} - \frac{{x^{'}}^{2}}{2}}{x^{2} + y^{2} + z^{2}}) - 2 (\frac{{y y}^{'} - \frac{{y^{'}}^{2}}{2}}{x^{2} + y^{2} + z^{2}})\}]}^{\frac{1}{2}}$

$= R \sqrt{1 - 2 (x x' - \frac{{x'}^{2}}{2}) / R^{2} - 2 (y y' - \frac{{y'}^{2}}{2}) / R^{2}} ≅ R (1 - x x' / R^{2} - y y' / R^{2})$ 式(1-10)

従って 1/r は

$\frac{1}{r} = \frac{1}{R (1 - x x' / R^{2} - y y' / R^{2})} ≅ \frac{1}{R} \{1 + \frac{1}{R^{2}} (x x' + y y')\}$ 式(1-11)

$\overset{⃑}{A} = \frac{μ_{0} ｉ}{4 π} \oint \frac{\overset{⃑}{d s'}}{r} ≅ \frac{μ_{0} ｉ}{4 π} \frac{1}{R} \oint \{1 + \frac{1}{R^{2}} (x x' + y y')\} \overset{⃑}{d s}'$ 式(1-12)

ここで経路積分の1項目はゼロになり、２項目の積分は

$\overset{⃑}{A} = \frac{μ_{0} ｉ}{4 π} \frac{1}{R^{3}} \oint ({x x}^{'} + {y y}^{'}) \overset{⃑}{d s}' = \frac{μ_{0} ｉ}{4 π} \frac{1}{R^{3}} (x \oint x' \overset{⃑}{d s} + y \oint y' \overset{⃑}{d s})$ 式(1-13)

式(1-13)の第一項目の経路積分は

$\oint x' \overset{⃑}{d s} = \oint x' {d s'}_{x} \overset{⃑}{e_{x}} + \oint x' {d s'}_{y} \overset{⃑}{e_{y}}$

となるが、一項目は経路積分の往きと帰りで同じ $x'$ の値に対し ${d s'}_{x}$ の符号が逆になるので積分はゼロとなる。（Fig.3参照）二項目は、環で囲まれた面積Sとなる事がFig.3より解る。次に、式(1-13)の第二項目の経路積分は

$\oint y' \overset{⃑}{d s} = \oint y' {d s'}_{x} \overset{⃑}{e_{x}} + \oint y' {d s'}_{y} \overset{⃑}{e_{y}}$

となるが、一項目は－S となる事が、Fig.3より解る。また二項目は経路積分の往きと帰りで同じ $y'$ の値に対し ${d s'}_{y}$ の符号が逆になるので積分はゼロとなる。従って式(1-13)は

$\overset{⃑}{A} = \frac{μ_{0} ｉ}{4 π} \frac{1}{R^{3}} (x \oint x' \overset{⃑}{d s'} + y \oint y' \overset{⃑}{d s'}) = \frac{μ_{0} ｉ}{4 π} \frac{1}{R^{3}} (x S \overset{⃑}{e_{y}} - y S \overset{⃑}{e_{x}})$

$= \frac{μ_{0} ｉ}{4 π} \frac{S}{R^{3}} (x \overset{⃑}{e_{y}} - y \overset{⃑}{e_{x}}) = \frac{μ_{0} ｉ}{4 π} \frac{S}{R^{3}} (x \overset{⃑}{e_{z}} \times \overset{⃑}{e_{x}} - y \overset{⃑}{e_{y}} \times \overset{⃑}{e_{z}})$

$= \frac{μ_{0} ｉ}{4 π} \frac{S}{R^{3}} \overset{⃑}{e_{z}} \times (x \overset{⃑}{e_{x}} + y \overset{⃑}{e_{y}})$ 式(1-14)

ここでベクトル積 $\overset{⃑}{e_{y}} \times \overset{⃑}{e_{z}} = - \overset{⃑}{e_{z}} \times \overset{⃑}{e_{y}}$ となる事を用いている。更に $\overset{⃑}{e_{z}} \times \overset{⃑}{e_{z}} = 0$ であるので、式(1-14)の右辺に $z (\overset{⃑}{e_{z}} \times \overset{⃑}{e_{z}})$ を加えても変わらないので

$\overset{⃑}{A} = \frac{μ_{0} ｉ}{4 π} \frac{S}{R^{3}} \overset{⃑}{e_{z}} \times (x \overset{⃑}{e_{x}} + y \overset{⃑}{e_{y}} + z \overset{⃑}{e_{z}}) = \frac{μ_{0} ｉ}{4 π} \frac{S}{R^{3}} \overset{⃑}{e_{z}} \times \overset{⃑}{R}$ 式(1-15)

ここに、以下の量を定義し、磁気双極子モーメントと呼ぶ。

$\overset{⃑}{m} = i S \overset{⃑}{e_{z}} = i \overset{⃑}{S}$ 式(1-16)

ここで $\overset{⃑}{S}$ は環の面の法線方向を向き、面積Sを持つベクトルである。式(1-15)は、磁気双極子モーメント $\overset{⃑}{m}$ を用いて

$\overset{⃑}{A} = \frac{μ_{0}}{4 π} \frac{1}{R^{3}} \overset{⃑}{m} \times \overset{⃑}{R}$ 式(1-17)

このように原点から距離 $\overset{⃑}{R}$ の点の磁気双極子モーメントによるベクトルポテンシャルを求める事ができた。環電流はXY平面にあると仮定したが、式(1-17)は、 $\overset{⃑}{m}$ と $\overset{⃑}{R}$ の外積の形に一般化されており、一般の場合にも成り立つ。磁場は式(1-17)の回転より求められる。以下のベクトル演算の一般公式を用いる。

$\overset{⃑}{\nabla} \times (\overset{⃑}{F} \times \overset{⃑}{G}) = \overset{⃑}{F} (\overset{⃑}{\nabla} ∙ \overset{⃑}{G}) - \overset{⃑}{G} (\overset{⃑}{\nabla} ∙ \overset{⃑}{F}) + (\overset{⃑}{G} ∙ \overset{⃑}{\nabla}) \overset{⃑}{F} - (\overset{⃑}{F} ∙ \overset{⃑}{\nabla}) \overset{⃑}{G}$ 式(1-18)

$\overset{⃑}{m}$ は一定なので $\overset{⃑}{\nabla} ∙ \overset{⃑}{m} = 0, (\frac{\overset{⃑}{R}}{R^{3}} ∙ \overset{⃑}{\nabla}) \overset{⃑}{m} = 0$ であるから、式(1-17)の回転は

$\overset{⃑}{B} = \overset{⃑}{\nabla} \times \overset{⃑}{A} = \frac{μ_{0}}{4 π} \overset{⃑}{\nabla} \times (\overset{⃑}{m} \times \frac{\overset{⃑}{R}}{R^{3}}) = \frac{μ_{0}}{4 π} \{\overset{⃑}{m} (\overset{⃑}{\nabla} ∙ \frac{\overset{⃑}{R}}{R^{3}}) - (\overset{⃑}{m} ∙ \overset{⃑}{\nabla}) \frac{\overset{⃑}{R}}{R^{3}}\}$

$= \frac{μ_{0}}{4 π} \{\overset{⃑}{m} (\frac{\partial}{\partial x} \frac{x}{{\sqrt{x^{2} + y^{2} + z^{2}}}^{3}} + \frac{\partial}{\partial y} \frac{y}{{\sqrt{x^{2} + y^{2} + z^{2}}}^{3}} + \frac{\partial}{\partial z} \frac{z}{{\sqrt{x^{2} + y^{2} + z^{2}}}^{3}})\}$

$- \frac{μ_{0}}{4 π} \{(m_{x} \frac{\partial}{\partial x} \frac{x}{{\sqrt{x^{2} + y^{2} + z^{2}}}^{3}} + m_{y} \frac{\partial}{\partial y} \frac{x}{{\sqrt{x^{2} + y^{2} + z^{2}}}^{3}} + m_{z} \frac{\partial}{\partial z} \frac{x}{{\sqrt{x^{2} + y^{2} + z^{2}}}^{3}}) \overset{⃑}{e_{x}}$

$+ (m_{x} \frac{\partial}{\partial x} \frac{y}{{\sqrt{x^{2} + y^{2} + z^{2}}}^{3}} + m_{y} \frac{\partial}{\partial y} \frac{y}{{\sqrt{x^{2} + y^{2} + z^{2}}}^{3}} + m_{z} \frac{\partial}{\partial z} \frac{y}{{\sqrt{x^{2} + y^{2} + z^{2}}}^{3}}) \overset{⃑}{e_{y}}$

$+ (m_{x} \frac{\partial}{\partial x} \frac{z}{{\sqrt{x^{2} + y^{2} + z^{2}}}^{3}} + m_{y} \frac{\partial}{\partial y} \frac{z}{{\sqrt{x^{2} + y^{2} + z^{2}}}^{3}} + m_{z} \frac{\partial}{\partial z} \frac{z}{{\sqrt{x^{2} + y^{2} + z^{2}}}^{3}}) \overset{⃑}{e_{z}}\}$ 式(1-19)

ここで一項目の｛　｝内は

$\frac{\partial}{\partial x} \frac{x}{{\sqrt{x^{2} + y^{2} + z^{2}}}^{3}} + \frac{\partial}{\partial y} \frac{y}{{\sqrt{x^{2} + y^{2} + z^{2}}}^{3}} + \frac{\partial}{\partial z} \frac{z}{{\sqrt{x^{2} + y^{2} + z^{2}}}^{3}} = \frac{3}{{\sqrt{x^{2} + y^{2} + z^{2}}}^{3}} - \frac{3 (x^{2} + y^{2} + z^{2})}{{\sqrt{x^{2} + y^{2} + z^{2}}}^{5}}$

$= \frac{3}{{\sqrt{x^{2} + y^{2} + z^{2}}}^{3}} - \frac{3}{{\sqrt{x^{2} + y^{2} + z^{2}}}^{3}} = 0$ 式(1-20)

となり、ゼロとなる。二項目の｛　｝内で一つ目の（　）内（ｘ成分）を考えると

$(m_{x} \frac{\partial}{\partial x} \frac{x}{{\sqrt{x^{2} + y^{2} + z^{2}}}^{3}} + m_{y} \frac{\partial}{\partial y} \frac{x}{{\sqrt{x^{2} + y^{2} + z^{2}}}^{3}} + m_{z} \frac{\partial}{\partial z} \frac{x}{{\sqrt{x^{2} + y^{2} + z^{2}}}^{3}})$

$= m_{x} (\frac{1}{{\sqrt{x^{2} + y^{2} + z^{2}}}^{3}} - \frac{3 x^{2}}{{\sqrt{x^{2} + y^{2} + z^{2}}}^{5}}) {- m}_{y} \frac{3 x y}{{\sqrt{x^{2} + y^{2} + z^{2}}}^{5}} {- m}_{z} \frac{3 x z}{{\sqrt{x^{2} + y^{2} + z^{2}}}^{5}}$

$= \frac{m_{x}}{{\sqrt{x^{2} + y^{2} + z^{2}}}^{3}} - \frac{3 x (m_{x} x + m_{y} y + m_{z} z)}{{\sqrt{x^{2} + y^{2} + z^{2}}}^{5}} = \frac{m_{x}}{R^{3}} - \frac{3 x \overset{⃑}{m} ∙ \overset{⃑}{R}}{R^{5}}$ 式(1-21)

よって式(1-19)は

$\overset{⃑}{B} = \frac{μ_{0}}{4 π} \{- \frac{\overset{⃑}{m}}{R^{3}} + \frac{3 \overset{⃑}{R} (\overset{⃑}{m} ∙ \overset{⃑}{R})}{R^{5}}\}$ 式(1-22)

ここで、

$\frac{\partial}{\partial x} (\frac{\overset{⃑}{m} ∙ \overset{⃑}{R}}{R^{3}}) = \frac{\partial}{\partial x} (\frac{m_{x} x + m_{y} y + m_{z} z}{{\sqrt{x^{2} + y^{2} + z^{2}}}^{3}}) = \frac{m_{x}}{{\sqrt{x^{2} + y^{2} + z^{2}}}^{3}} - \frac{3 x (m_{x} x + m_{y} y + m_{z} z)}{{\sqrt{x^{2} + y^{2} + z^{2}}}^{5}}$ 式(1-23)

と書けるので、式(1-22)は

$\overset{⃑}{B} = - μ_{0}$ $\overset{⃑}{\nabla} (\frac{\overset{⃑}{m} ∙ \overset{⃑}{R}}{{4 π R}^{3}})$ 式(1-24)

と表す事ができる。

--------磁石専用磁場計算アプリケーション(Kojimag)に興味がある方はこちらへ--------

このサイトの基礎計算式を基に磁石専用アプリケーションを開発しました。
こちらから”磁石専用磁場計算アプリケーション(Kojimag)”からKojimagの詳細について確認できます。