§1-3)磁性体を含む場合（ベクトルポテンシャルの表式）

§１．磁性体を含む系の磁場の表式

３）磁性体を含む場合（ベクトルポテンシャルの表式）

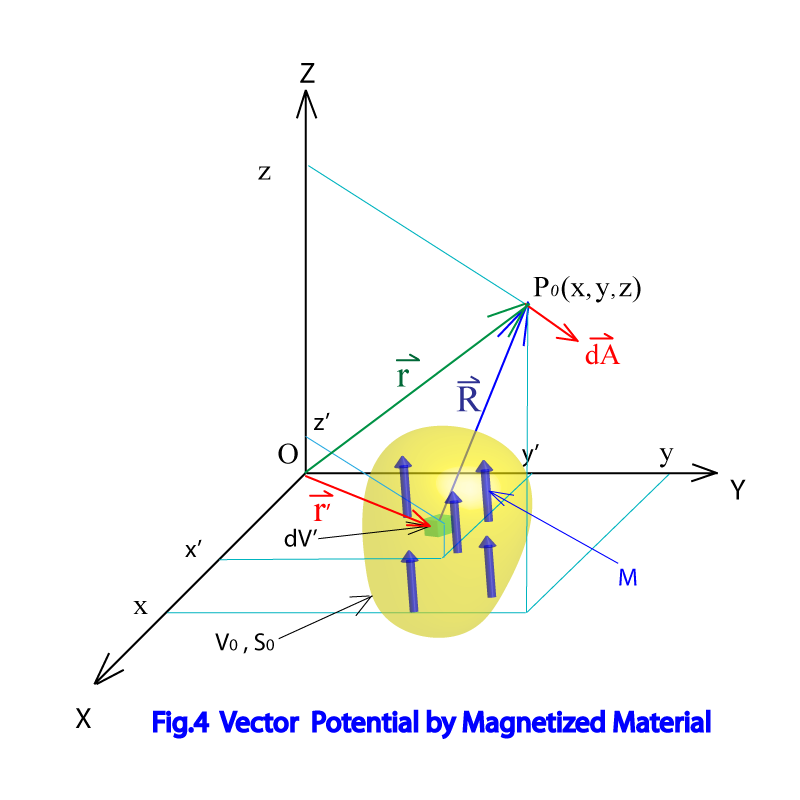
次に磁性体を含む場合の磁場の表式を考える。Fig.4に示した様に、 $V_{0}$ の領域に広がっている、表面 $S_{0}$ を持った物体の中に、磁気双極子モーメント $\overset{⃑}{m_{i}}$ が含まれているとする。物体の中の微小領域dV’に含まれる単位体積当たりの磁気双極子モーメント

$\overset{⃑}{M} = \frac{1}{d V} \sum_{i} \overset{⃑}{m_{i}}$ 式(1-25)

を磁化と呼ぶ。２)において、磁気双極子モーメントが作るベクトルポテンシャルは式(1-17)で現わす事ができる事がわかっているので、Fig.4の物体全体が点 $P_{0}$ に作るベクトルポテンシャルは

$\overset{⃑}{A} (x, y, z) = \frac{μ_{0}}{4 π} ∭_{V_{0}}^{} \frac{1}{R^{3}} \overset{⃑}{M} \times \overset{⃑}{R} d V'$ 式(1-26)

と表す事ができる。Fig.4より、

$\begin{matrix} \overset{⃑}{R} = \overset{⃑}{r} - {\overset{⃑}{r}}^{'} = (x - x^{'}, y - y^{'}, z - z') \\ R = \sqrt{{(x - x^{'})}^{2} + {(y - y^{'})}^{2} + {(z - z^{'})}^{2}} \end{matrix}\}$ 式(1-27)

であるので

磁性体によるベクトルポテンシャル

$\overset{⃑}{\nabla} \frac{1}{R} = \frac{\partial}{\partial x} \frac{1}{\sqrt{{(x - x^{'})}^{2} + {(y - y^{'})}^{2} + {(z - z^{'})}^{2}}} \overset{⃑}{e_{x}} + \frac{\partial}{\partial y} \frac{1}{\sqrt{{(x - x^{'})}^{2} + {(y - y^{'})}^{2} + {(z - z^{'})}^{2}}} \overset{⃑}{e_{y}} + \frac{\partial}{\partial z} \frac{1}{\sqrt{{(x - x^{'})}^{2} + {(y - y^{'})}^{2} + {(z - z^{'})}^{2}}} \overset{⃑}{e_{z}}$

$= - \frac{x - x'}{{\sqrt{{(x - x^{'})}^{2} + {(y - y^{'})}^{2} + {(z - z^{'})}^{2}}}^{3}} \overset{⃑}{e_{x}} - \frac{y - y'}{{\sqrt{{(x - x^{'})}^{2} + {(y - y^{'})}^{2} + {(z - z^{'})}^{2}}}^{3}} \overset{⃑}{e_{y}} - \frac{z - z'}{{\sqrt{{(x - x^{'})}^{2} + {(y - y^{'})}^{2} + {(z - z^{'})}^{2}}}^{3}} \overset{⃑}{e_{z}}$

$= - \frac{\overset{⃑}{R}}{R^{3}}$ 式(1-28)

ここで式(1-28)の $\overset{⃑}{\nabla}$ を ${\overset{⃑}{\nabla}}^{'} = \frac{\partial}{\partial x'} \overset{⃑}{e_{x}} + \frac{\partial}{\partial y'} \overset{⃑}{e_{x}} + \frac{\partial}{\partial z'} \overset{⃑}{e_{x}}$ に置き換えると

$\overset{⃑}{\nabla}' \frac{1}{R} = \frac{\partial}{\partial x'} \frac{1}{\sqrt{{(x - x^{'})}^{2} + {(y - y^{'})}^{2} + {(z - z^{'})}^{2}}} \overset{⃑}{e_{x}} + \frac{\partial}{\partial y'} \frac{1}{\sqrt{{(x - x^{'})}^{2} + {(y - y^{'})}^{2} + {(z - z^{'})}^{2}}} \overset{⃑}{e_{y}} + \frac{\partial}{\partial z'} \frac{1}{\sqrt{{(x - x^{'})}^{2} + {(y - y^{'})}^{2} + {(z - z^{'})}^{2}}} \overset{⃑}{e_{z}}$

$= - \frac{- (x - x')}{{\sqrt{{(x - x^{'})}^{2} + {(y - y^{'})}^{2} + {(z - z^{'})}^{2}}}^{3}} \overset{⃑}{e_{x}} - \frac{- (y - y')}{{\sqrt{{(x - x^{'})}^{2} + {(y - y^{'})}^{2} + {(z - z^{'})}^{2}}}^{3}} \overset{⃑}{e_{y}} - \frac{- (z - z')}{{\sqrt{{(x - x^{'})}^{2} + {(y - y^{'})}^{2} + {(z - z^{'})}^{2}}}^{3}} \overset{⃑}{e_{z}}$

$= - \overset{⃑}{\nabla} \frac{1}{R}$ 式(1-29)

となる事がわかるので式(1-26)は

$\overset{⃑}{A} (x, y, z) = \frac{μ_{0}}{4 π} ∭_{V_{0}}^{} \overset{⃑}{M} \times (\overset{⃑}{\nabla}' \frac{1}{R}) d V'$ 式(1-30)

と表す事ができる。ここで次のベクトル演算の公式を用いる。

$\begin{matrix} \overset{⃑}{\nabla} φ \times \overset{⃑}{F} = \overset{⃑}{\nabla} \times (φ \overset{⃑}{F}) - φ (\overset{⃑}{\nabla} \times \overset{⃑}{F}) \\ ∭_{V_{0}}^{} \overset{⃑}{\nabla} \times \overset{⃑}{F} d V = - \iint_{S_{0}}^{} \overset{⃑}{F} \times \overset{⃑}{n} d A \end{matrix}\}$ 式(1-31)

（ $\overset{⃑}{n}$ は　体積 $V_{0}$ の表面 $S_{0}$ 上の微小面積要素 dA の単位法線ベクトルである。）式(1-30)の積分の中は、式(1-31)の上側の式を用いて

$\overset{⃑}{M} \times (\overset{⃑}{\nabla}' \frac{1}{R}) = - (\overset{⃑}{\nabla}' \frac{1}{R}) \times \overset{⃑}{M} = - \{\overset{⃑}{\nabla}' \times (\frac{1}{R} \overset{⃑}{M}) - \frac{1}{R} (\overset{⃑}{\nabla}' \times \overset{⃑}{M})\}$ 式(1-32)

従って式(1-30)は

$\overset{⃑}{A} (x, y, z) = - \frac{μ_{0}}{4 π} ∭_{V_{0}}^{} {\overset{⃑}{\nabla}}^{'} \times (\frac{1}{R} \overset{⃑}{M}) {d V}^{'} + \frac{μ_{0}}{4 π} ∭_{V_{0}}^{} \frac{1}{R} (\overset{⃑}{\nabla}' \times \overset{⃑}{M}) d V'$ 式(1-33)

次に、上式において、式(1-31)の下側の式を用いると

$\overset{⃑}{A} (x, y, z) = \frac{μ_{0}}{4 π} \iint_{S_{0}}^{} \frac{1}{R} \overset{⃑}{M} \times \overset{⃑}{n} {d A}^{'} + \frac{μ_{0}}{4 π} ∭_{V_{0}}^{} \frac{1}{R} (\overset{⃑}{\nabla}' \times \overset{⃑}{M}) d V'$ 式(1-34)

ここで、V_0内の磁化Mに対応する等価電流密度として

$\overset{⃑}{J_{M}} = \overset{⃑}{\nabla}' \times M$ 式(1-35)

表面S_0上の磁化に対応する等価表面電流密度として　

$\overset{⃑}{j_{M}} = \overset{⃑}{M} \times \overset{⃑}{n}$ 式(1-36)

と定義すると、式(1-34)は

$\overset{⃑}{A} (x, y, z) = \frac{μ_{0}}{4 π} \iint_{S_{0}}^{} \frac{1}{R} \overset{⃑}{j_{M}} {d A}^{'} + \frac{μ_{0}}{4 π} ∭_{V_{0}}^{} \frac{1}{R} \overset{⃑}{J_{M}} d V'$ 式(1-37)

と定式化する事ができた。実際に、上式から回転をとれば磁場が求められるが、ベクトルポテンシャルはベクトル量であり実際の磁場の計算は煩雑になる為、次の項で、直接磁場を式(1-26)から求める事とする。

--------磁石専用磁場計算アプリケーション(Kojimag)に興味がある方はこちらへ--------

このサイトの基礎計算式を基に磁石専用アプリケーションを開発しました。
こちらから”磁石専用磁場計算アプリケーション(Kojimag)”からKojimagの詳細について確認できます。