§1-4）磁性体を含む場合（磁場の表式）

§１．磁性体を含む系の磁場の表式

４）磁性体を含む場合（磁場の表式）

式(1-26)の回転をとり直接磁場を求める事を考える

$\overset{⃑}{B} (x, y, z) = \overset{⃑}{\nabla} \times \overset{⃑}{A} (x, y, z) = \frac{μ_{0}}{4 π} ∭_{V_{0}}^{} \overset{⃑}{\nabla} \times \{\frac{1}{R^{3}} \overset{⃑}{M} (x^{'}, y^{'}, z') \times \overset{⃑}{R}\} d V'$ 式(1-38)

以下のベクトル演算の一般公式を用いる。

$\overset{⃑}{\nabla} \times (\overset{⃑}{F} \times \overset{⃑}{G}) = \overset{⃑}{F} (\overset{⃑}{\nabla} ∙ \overset{⃑}{G}) - \overset{⃑}{G} (\overset{⃑}{\nabla} ∙ \overset{⃑}{F}) + (\overset{⃑}{G} ∙ \overset{⃑}{\nabla}) \overset{⃑}{F} - (\overset{⃑}{F} ∙ \overset{⃑}{\nabla}) \overset{⃑}{G}$ 式(1-39)

式(1-38)の積分の中は $\overset{⃑}{F}$ に $\overset{⃑}{M}$ 、 $\overset{⃑}{G}$ に $\overset{⃑}{\frac{R}{R^{3}}}$ を代入すると

$\overset{⃑}{\nabla} \times (\frac{1}{R^{3}} \overset{⃑}{M} \times \overset{⃑}{R}) = \overset{⃑}{M} (\overset{⃑}{\nabla} ∙ \overset{⃑}{\frac{R}{R^{3}}}) - \overset{⃑}{\frac{R}{R^{3}}} (\overset{⃑}{\nabla} ∙ \overset{⃑}{M}) + (\overset{⃑}{\frac{R}{R^{3}}} ∙ \overset{⃑}{\nabla}) \overset{⃑}{M} - (\overset{⃑}{M} ∙ \overset{⃑}{\nabla}) \overset{⃑}{\frac{R}{R^{3}}}$ 式(1-40)

となるが、 $\overset{⃑}{M}$ は $(x^{'}, y^{'}, z')$ の関数であるので、式(1-40)の2項目の $\overset{⃑}{\nabla} ∙ \overset{⃑}{M}$ 及び3項目の $(\overset{⃑}{R} ∙ \overset{⃑}{\nabla}) \overset{⃑}{M}$ はゼロとなる。従って式(1-38)は

$\overset{⃑}{B} (x, y, z) = \frac{μ_{0}}{4 π} ∭_{V_{0}}^{} \overset{⃑}{\nabla} \times \{\frac{1}{R^{3}} \overset{⃑}{M} (x^{'}, y^{'}, z') \times \overset{⃑}{R}\} d V'$

$= \frac{μ_{0}}{4 π} ∭_{V_{0}}^{} \{\overset{⃑}{M} (\overset{⃑}{\nabla} ∙ \overset{⃑}{\frac{R}{R^{3}}}) - (\overset{⃑}{M} ∙ \overset{⃑}{\nabla}) \overset{⃑}{\frac{R}{R^{3}}}\} d V'$ 式(1-41)

式(1-41)の積分内の第一項目の（　）内は $\overset{⃑}{R} = (x - x^{'}, y - y^{'}, z - z') \neq \overset{⃑}{0}$ であれば

$\overset{⃑}{\nabla} ∙ \overset{⃑}{\frac{R}{R^{3}}} = \frac{\partial}{\partial x} \frac{x - x'}{{\sqrt{{(x - x^{'})}^{2} + {(y - y^{'})}^{2} + {(z - z^{'})}^{2}}}^{3}} + \frac{\partial}{\partial y} \frac{y - y'}{{\sqrt{{(x - x^{'})}^{2} + {(y - y^{'})}^{2} + {(z - z^{'})}^{2}}}^{3}} + \frac{\partial}{\partial z} \frac{z - z'}{{\sqrt{{(x - x^{'})}^{2} + {(y - y^{'})}^{2} + {(z - z^{'})}^{2}}}^{3}}$

$= \frac{3}{{\sqrt{{(x - x^{'})}^{2} + {(y - y^{'})}^{2} + {(z - z^{'})}^{2}}}^{3}} - \frac{3 \{{(x - x^{'})}^{2} + {(y - y^{'})}^{2} + {(z - z^{'})}^{2}\}}{{\sqrt{{(x - x^{'})}^{2} + {(y - y^{'})}^{2} + {(z - z^{'})}^{2}}}^{5}} = 0$ 式(1-42)

が成り立つ。

従って積分の領域をFig.5に示した様に、点 $\overset{⃑}{P_{0}} = \overset{⃑}{r} = (x, y, z)$ を含む球の領域 $V_{1}$ とそれ以外の領域 $V_{0} － V_{1}$ に分けて考える。

積分領域

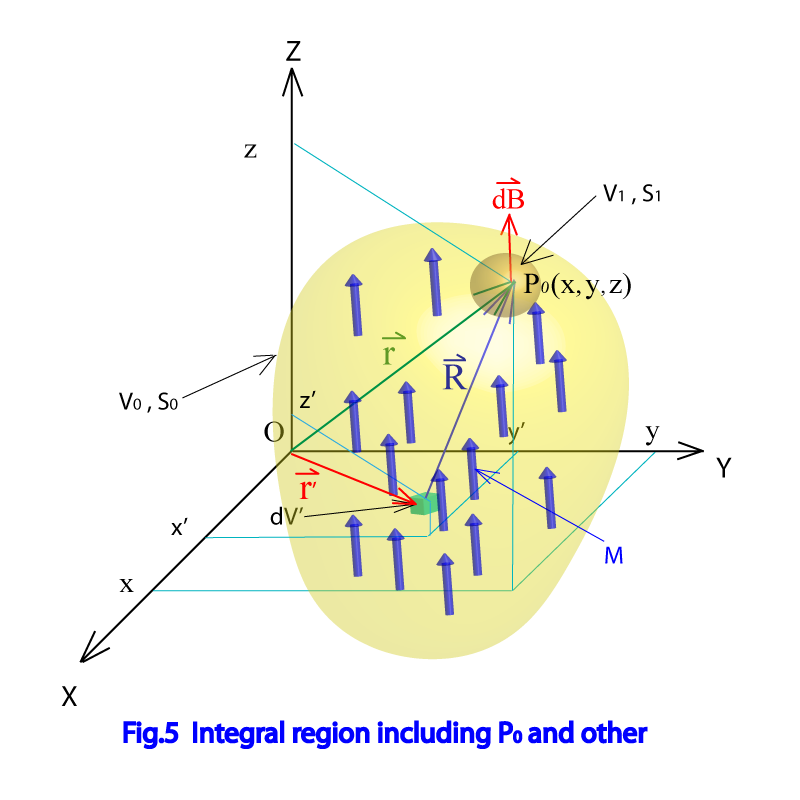
領域 $V_{0} － V_{1}$ では、式(1-42)が成り立つので式(1-41)の積分の第一項は　

$\frac{μ_{0}}{4 π} ∭_{V_{0}}^{} \overset{⃑}{M} (\overset{⃑}{\nabla} ∙ \overset{⃑}{\frac{R}{R^{3}}}) {d V}^{'} = \frac{μ_{0}}{4 π} ∭_{V_{1}}^{} \overset{⃑}{M} (\overset{⃑}{\nabla} ∙ \overset{⃑}{\frac{R}{R^{3}}}) {d V}^{'} + \frac{μ_{0}}{4 π} ∭_{V_{0} - V_{1}}^{} \overset{⃑}{M} (\overset{⃑}{\nabla} ∙ \overset{⃑}{\frac{R}{R^{3}}}) {d V}^{'}$

$= \frac{μ_{0}}{4 π} ∭_{V_{1}}^{} \overset{⃑}{M} (\overset{⃑}{\nabla} ∙ \overset{⃑}{\frac{R}{R^{3}}}) {d V}^{'}$ 式(1-43)

$V_{1}$ の領域を十分小さくとれば $\overset{⃑}{M}$ は一定値 $\overset{⃑}{M} (x, y, z)$ に近づくので式(1-43)は

$\frac{μ_{0}}{4 π} ∭_{V_{1}}^{} \overset{⃑}{M} (\overset{⃑}{\nabla} ∙ \overset{⃑}{\frac{R}{R^{3}}}) {d V}^{'} = - \frac{μ_{0}}{4 π} \overset{⃑}{M} (x, y, z) ∭_{V_{1}}^{} \overset{⃑}{M} (\overset{⃑}{\nabla'} ∙ \overset{⃑}{\frac{R}{R^{3}}}) d V'$ 式(1-44)

ここでベクトル演算の公式

$∭_{V_{0}}^{} \overset{⃑}{\nabla} ∙ \overset{⃑}{F} d V = \iint_{S_{0}}^{} \overset{⃑}{F} ∙ \overset{⃑}{n} d A$ 式(1-45)

を用いると式(1-44)は

$- \frac{μ_{0}}{4 π} \overset{⃑}{M} (x, y, z) ∭_{V_{1}}^{} (\overset{⃑}{\nabla}' ∙ \overset{⃑}{\frac{R}{R^{3}}}) {d V}^{'} = \frac{μ_{0}}{4 π} \overset{⃑}{M} (x, y, z) \iint_{S_{1}}^{} \overset{⃑}{\frac{S}{S^{3}}} ∙ \overset{⃑}{n} d A'$ 式(1-46)

ここで $\overset{⃑}{S}$ は領域 $V_{1}$ の中心から球面 $S_{1}$ 上へのベクトルであり、 $\overset{⃑}{n}$ は球面 $S_{1}$ 上の微小面積要素 $d A'$ の単位法線ベクトルであり、

$\iint_{S_{1}}^{} \overset{⃑}{S} ∙ \overset{⃑}{n} d A' = 4 π S^{3}$ 式(1-47)

であるから、式(1-46)は

$\frac{μ_{0}}{4 π} \overset{⃑}{M} (x, y, z) \iint_{S_{1}}^{} \overset{⃑}{\frac{S}{S^{3}}} ∙ \overset{⃑}{n} d A' = μ_{0} \overset{⃑}{M} (x, y, z)$ 式(1-48)

従って式(1-41)の｛　｝内の第一項は

$\frac{μ_{0}}{4 π} ∭_{V_{0}}^{} \overset{⃑}{M} (\overset{⃑}{\nabla} ∙ \overset{⃑}{\frac{R}{R^{3}}}) {d V}^{'} = μ_{0} \overset{⃑}{M} (x, y, z)$ 式(1-49)

と表せる事がわかる。

次に、式(1-41)の｛　｝内の第二項目は以下のベクトル演算公式

$\overset{⃑}{\nabla} (\overset{⃑}{F} ∙ \overset{⃑}{G}) = (\overset{⃑}{F} ∙ \overset{⃑}{\nabla}) \overset{⃑}{G} + (\overset{⃑}{G} ∙ \overset{⃑}{\nabla}) \overset{⃑}{F} + \overset{⃑}{F} \times (\overset{⃑}{\nabla} \times \overset{⃑}{G}) + \overset{⃑}{G} \times (\overset{⃑}{\nabla} \times \overset{⃑}{F})$ 式(1-50)

を用いる。上式の $\overset{⃑}{F}$ に $\overset{⃑}{M}$ 、 $\overset{⃑}{G}$ に $\overset{⃑}{\frac{R}{R^{3}}}$ を代入すると

$\overset{⃑}{\nabla} (\overset{⃑}{M} ∙ \overset{⃑}{\frac{R}{R^{3}}}) = (\overset{⃑}{M} ∙ \overset{⃑}{\nabla}) \overset{⃑}{\frac{R}{R^{3}}} + (\overset{⃑}{\frac{R}{R^{3}}} ∙ \overset{⃑}{\nabla}) \overset{⃑}{M} + \overset{⃑}{M} \times (\overset{⃑}{\nabla} \times \overset{⃑}{\frac{R}{R^{3}}}) + \overset{⃑}{\frac{R}{R^{3}}} \times (\overset{⃑}{\nabla} \times \overset{⃑}{M})$ 式(1-51)

$\overset{⃑}{M}$ は $(x^{'}, y^{'}, z')$ の関数であるので、式(1-51)の2項目の $(\overset{⃑}{R} ∙ \overset{⃑}{\nabla}) \overset{⃑}{M}$ 及び4項目の $\overset{⃑}{\nabla} \times \overset{⃑}{M}$ はゼロとなる。また3項目の括弧内は以下の様に勾配の回転となるのでゼロとなる。

$\overset{⃑}{\nabla} \times \overset{⃑}{\frac{R}{R^{3}}} = \overset{⃑}{\nabla} \times (- \overset{⃑}{\nabla} \frac{1}{R}) = \overset{⃑}{0}$ 式(1-52)

従って式(1-51)は以下の様になる。

$\overset{⃑}{\nabla} (\overset{⃑}{M} ∙ \overset{⃑}{\frac{R}{R^{3}}}) = (\overset{⃑}{M} ∙ \overset{⃑}{\nabla}) \overset{⃑}{\frac{R}{R^{3}}}$ 式(1-53)

よって式(1-41)の2項目の積分は

$- \frac{μ_{0}}{4 π} ∭_{V_{0}}^{} \{\overset{⃑}{M} (x^{'}, y^{'}, z') ∙ \overset{⃑}{\nabla}\} \overset{⃑}{\frac{R}{R^{3}}} {d V}^{'} = - \overset{⃑}{\nabla} \frac{μ_{0}}{4 π} ∭_{V_{0}}^{} (\overset{⃑}{M} (x^{'}, y^{'}, z') ∙ \overset{⃑}{\frac{R}{R^{3}}}) {d V}^{'}$ 式(1-54)

ここで積分の中を考えると

$\overset{⃑}{M} (x^{'}, y^{'}, z') ∙ \overset{⃑}{\frac{R}{R^{3}}} = \overset{⃑}{M} (x^{'}, y^{'}, z') ∙ \frac{\overset{⃑}{r} - \overset{⃑}{r'}}{{|\overset{⃑}{r} - \overset{⃑}{r'}|}^{3}} = \overset{⃑}{M} (x^{'}, y^{'}, z') ∙ \overset{⃑}{\nabla}' (\frac{1}{R})$ 式(1-54')

ここで、 $\overset{⃑}{\nabla}'$ は、 $x,^{'}, y^{'}, z'$ に関する微分演算子である事に注意する事。

${\overset{⃑}{\nabla}}^{'} = \frac{\partial}{\partial x'} \overset{⃑}{e_{x}} + \frac{\partial}{\partial y'} \overset{⃑}{e_{y}} + \frac{\partial}{\partial z'} \overset{⃑}{e_{z}}$ 式(1-55)

更に

${\overset{⃑}{\nabla}}^{'} ∙ \frac{\overset{⃑}{M} (x^{'}, y^{'}, z')}{R} = \frac{1}{R} {\overset{⃑}{\nabla}}^{'} ∙ \overset{⃑}{M} (x^{'}, y^{'}, z') + \overset{⃑}{M} (x^{'}, y^{'}, z') ∙ {\overset{⃑}{\nabla}}^{'} (\frac{1}{R})$ 式(1-56)

であるので式(1-54)は

$- \frac{μ_{0}}{4 π} ∭_{V_{0}}^{} \{\overset{⃑}{M} (x^{'}, y^{'}, z') ∙ \overset{⃑}{\nabla}\} \overset{⃑}{\frac{R}{R^{3}}} {d V}^{'}$

$= - \overset{⃑}{\nabla} \frac{μ_{0}}{4 π} ∭_{V_{0}}^{} ({\overset{⃑}{\nabla}}^{'} ∙ \frac{\overset{⃑}{M} (x^{'}, y^{'}, z')}{R} - \frac{1}{R} {\overset{⃑}{\nabla}}^{'} ∙ \overset{⃑}{M} (x^{'}, y^{'}, z')) {d V}^{'}$ 式(1-57)

積分の一項目にベクトル演算の公式(1-45)を用いると式(1-56)は

$- \frac{μ_{0}}{4 π} ∭_{V_{0}}^{} \{\overset{⃑}{M} (x^{'}, y^{'}, z') ∙ \overset{⃑}{\nabla}\} \overset{⃑}{\frac{R}{R^{3}}} {d V}^{'}$

$= - \overset{⃑}{\nabla} \frac{μ_{0}}{4 π} \iint_{S_{0}}^{} \frac{\overset{⃑}{M} (x^{'}, y^{'}, z') ∙ \overset{⃑}{n}}{R} {d A}^{'} + \overset{⃑}{\nabla} \frac{μ_{0}}{4 π} ∭_{V_{0}}^{} \frac{{\overset{⃑}{\nabla}}^{'} ∙ \overset{⃑}{M} (x^{'}, y^{'}, z')}{R} {d V}^{'}$ 式(1-58)

と表す事ができ、ここで、磁極密度

$ρ_{M} (x^{'}, y^{'}, z') \equiv - {\overset{⃑}{\nabla}}^{'} ∙ \overset{⃑}{M} (x^{'}, y^{'}, z')$ 式(1-59)

及び表面磁極密度

$σ_{M} (x^{'}, y^{'}, z') \equiv \overset{⃑}{M} (x^{'}, y^{'}, z') ∙ \overset{⃑}{n}$ 式(1-60)

を定義すると、式(1-41)は

$\overset{⃑}{B} (x, y, z) = \frac{μ_{0}}{4 π} ∭_{V_{0}}^{} \overset{⃑}{\nabla} \times \{\frac{1}{R^{3}} \overset{⃑}{M} (x^{'}, y^{'}, z') \times \overset{⃑}{R}\} d V'$

$= - \overset{⃑}{\nabla} \frac{μ_{0}}{4 π} \iint_{S_{0}}^{} \frac{σ_{M} (x^{'}, y^{'}, z')}{R} {d A}^{'} - \overset{⃑}{\nabla} \frac{μ_{0}}{4 π} ∭_{V_{0}}^{} \frac{ρ_{M} (x^{'}, y^{'}, z')}{R} {d V}^{'} ＋ μ_{0} \overset{⃑}{M} (x, y, z)$

$= \frac{μ_{0}}{4 π} \iint_{S_{0}}^{} σ_{M} (x^{'}, y^{'}, z') \frac{\overset{⃑}{R}}{R^{3}} {d A}^{'} + \frac{μ_{0}}{4 π} ∭_{V_{0}}^{} ρ_{M} (x^{'}, y^{'}, z') \frac{\overset{⃑}{R}}{R^{3}} {d V}^{'} ＋ μ_{0} \overset{⃑}{M} (x, y, z)$ 式(1-61)

と表す事ができた。

ここで一項目は磁性体の表面の磁極密度からの磁場への寄与を表し、2項目は磁性体内部の磁極密度からの磁場への寄与を表し、3項目は磁性体の磁化を表す。3項目は、点(x,y,z)　が磁性体の外部で真空であれば、ゼロとなる。

--------磁石専用磁場計算アプリケーション(Kojimag)に興味がある方はこちらへ--------

このサイトの基礎計算式を基に磁石専用アプリケーションを開発しました。
こちらから”磁石専用磁場計算アプリケーション(Kojimag)”からKojimagの詳細について確認できます。