§１２．全体座標系と固有座標系１）座標系の回転

§１２．全体座標系と固有座標系

１）座標系の回転

Fig.19に示したように全体座標系XYZ において　X軸の周りに角度 $θ_{x}$ の回転を行った後、回転後の座標系 $X^{'}, Y^{'}, Z^{'}$ の $Y'$ 軸の周りに角度 $θ_{y}$ の回転を行い、更にその回転後の座標系 $X ", Y ", Z "$ の $Z "$ 軸の周りに角度 $θ_{z}$ の回転を行い、座標系 $X "', Y'", Z "'$ になったとする。全体座標系XYZの点 $P (X_{0}, Y_{0}, Z_{0})$ は座標系XYZに固定しているとして、各回転後の座標系 $X^{'}, Y^{'}, Z^{'}$ 、 $X ", Y ", Z "$ 、 $X "', Y'", Z "'$ で $P (X_{0}', Y_{0}', Z_{0}')$ , $P (X_{0}'', Y_{0}'', Z_{0}'')$ , $P (X_{0}''', Y_{0}''', Z_{0}''')$ と表されるとする。

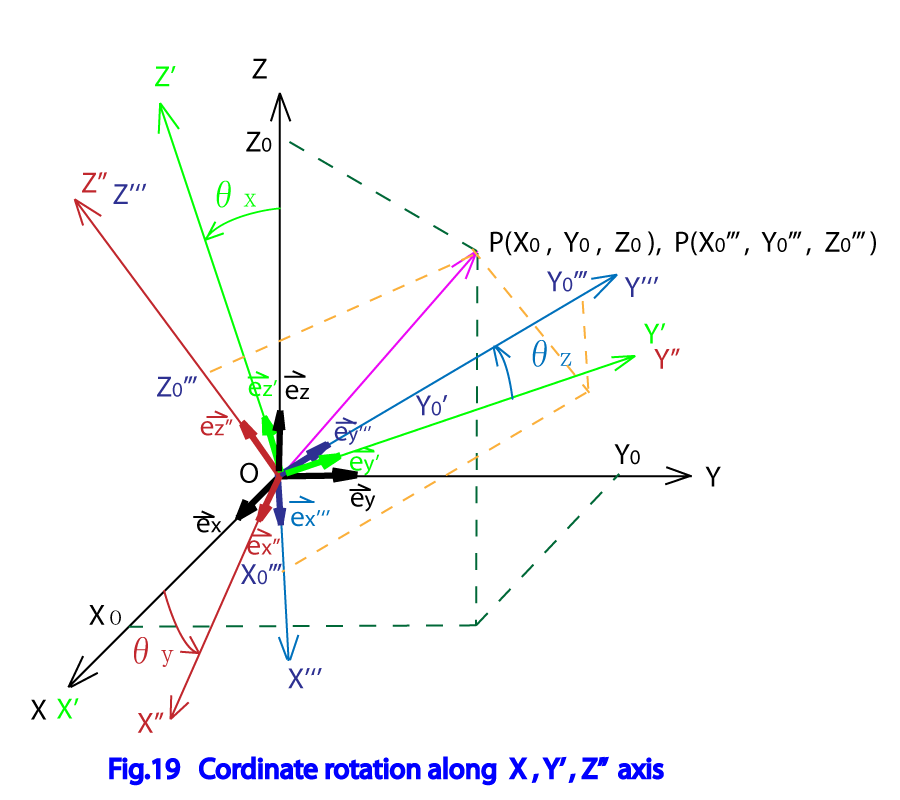
X,Y,Z軸の周りの座標系の回転

Fig.20に夫々の軸 $Z$ 、 $Y^{'}$ 、 $X "$ 　の周りに座標系を回転させた時の各軸の方向を向いた単位ベクトルの関係を示した。

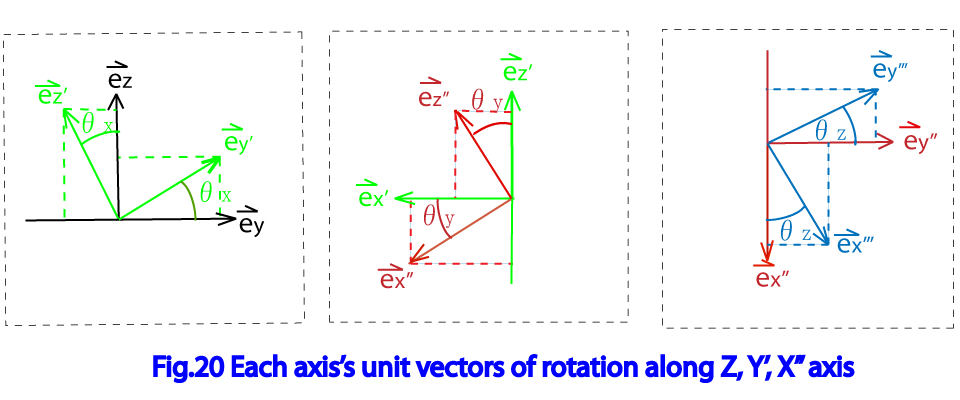
X,Y,Z軸の周りの座標系の回転

$\overset{⃑}{e_{x}}, \overset{⃑}{e_{y}}, \overset{⃑}{e_{z}}$ をX,Y,Z軸方向の単位ベクトルとし、 $\overset{⃑}{e_{x'}}, \overset{⃑}{e_{y'}}, \overset{⃑}{e_{z'}}$ 　をX’,Y’,Z’ 軸方向の単位ベクトルとするとX軸の周りに角度 $θ_{x}$ の回転させた時Fig.20 より

$\begin{matrix} \overset{⃑}{e_{x'}} = \overset{⃑}{e_{x}} \\ \overset{⃑}{e_{y'}} = \cos θ_{x} \overset{⃑}{e_{y}} + \sin θ_{x} \overset{⃑}{e_{z}} \\ \overset{⃑}{e_{z'}} = - \sin θ_{x} \overset{⃑}{e_{y}} + \cos θ_{x} \overset{⃑}{e_{z}} \end{matrix}\}$ 式(12-1)

式（12-1) を $\overset{⃑}{e_{x}}$ 　,　 $\overset{⃑}{e_{y}}$ 　,　 $\overset{⃑}{e_{z}}$ 　について解くと

$\begin{matrix} \overset{⃑}{e_{x}} = \overset{⃑}{e_{x'}} \\ \overset{⃑}{e_{y}} = \cos θ_{x} \overset{⃑}{e_{y'}} - \sin θ_{x} \overset{⃑}{e_{z'}} \\ \overset{⃑}{e_{z}} = \sin θ_{x} \overset{⃑}{e_{y'}} + \cos θ_{x} \overset{⃑}{e_{z'}} \end{matrix}\}$ 式(12-2)

また、点Pの座標はXYZ座標系で $(X_{0}, Y_{0}, Z_{0})$ と表されるので式（12-2)を用いて

$\overset{⃑}{O P}$ ＝ $X_{0} \overset{⃑}{e_{x}} + Y_{0} \overset{⃑}{e_{y}} + Z_{0} \overset{⃑}{e_{z}}$

　　＝ $X_{0} \overset{⃑}{e_{x'}} + Y_{0} (\cos θ_{x} \overset{⃑}{e_{y'}} - \sin θ_{x} \overset{⃑}{e_{z'}}) + Z_{0} (\sin θ_{x} \overset{⃑}{e_{y'}} + \cos θ_{x} \overset{⃑}{e_{z'}})$

　　＝ $X_{0} \overset{⃑}{e_{x'}} + (Y_{0} {c o s θ}_{x} + Z_{0} {s i n θ}_{x}) \overset{⃑}{e_{y'}} + ({- Y}_{0} {s i n θ}_{x} + Z_{0} {c o s θ}_{x}) \overset{⃑}{e_{z'}}$

　　＝ $X_{0}^{'} \overset{⃑}{e_{x'}} + Y_{0}^{'} \overset{⃑}{e_{y'}} + Z_{0}^{'} \overset{⃑}{e_{z'}}$ 式(12-3)

　従って

$\begin{matrix} X_{0}^{'} = X_{0} \\ Y_{0}^{'} = Y_{0} {c o s θ}_{x} + Z_{0} {s i n θ}_{x} \\ Z_{0}^{'} = {- Y}_{0} {s i n θ}_{x} + Z_{0} {c o s θ}_{x} \end{matrix}\}$ 式(12-4)

　逆に解くと

$\begin{matrix} X_{0} = X_{0}^{'} \\ Y_{0} = Y_{0}^{'} {c o s θ}_{x} - Z_{0}^{'} {s i n θ}_{x} \\ Z_{0} = Y_{0}^{'} {s i n θ}_{x} + Z_{0}^{'} {c o s θ}_{x} \end{matrix}\}$ 式(12-5)

次にY’ 軸の周りに $θ_{y}$ 　回転させるとFig.20　より

$\begin{matrix} \overset{⃑}{e_{x''}} = \cos θ_{y} \overset{⃑}{e_{x'}} - \sin θ_{y} \overset{⃑}{e_{z'}} \\ \overset{⃑}{e_{y''}} = \overset{⃑}{e_{y'}} \\ \overset{⃑}{e_{z^{''}}} = \sin θ_{y} \overset{⃑}{e_{x'}} + \cos θ_{y} \overset{⃑}{e_{z'}} \end{matrix}\}$ 式(12-6)

式（12-6) を $\overset{⃑}{e_{x'}}$ ,　 $\overset{⃑}{e_{y'}}$ ,　 $\overset{⃑}{e_{z'}}$ 　について解くと

$\begin{matrix} \overset{⃑}{e_{x'}} = \cos θ_{y} \overset{⃑}{e_{x''}} + \sin θ_{y} \overset{⃑}{e_{z''}} \\ \overset{⃑}{e_{y'}} = \overset{⃑}{e_{y''}} \\ \overset{⃑}{e_{z'}} = - \sin θ_{y} \overset{⃑}{e_{x''}} + \cos θ_{y} \overset{⃑}{e_{z''}} \end{matrix}\}$ 式(12-7)

また、Pの座標はXYZ座標系で $(X_{0}^{''}, Y_{0}^{''}, Z_{0}^{''})$ と表せるので式（12-7）を用いて

$\overset{⃑}{O P}$ ＝ $X_{0}^{'} \overset{⃑}{e_{x'}} + Y_{0}^{'} \overset{⃑}{e_{y'}} + Z_{0}^{'} \overset{⃑}{e_{z'}}$

　　＝ $X_{0}^{'} (\cos θ_{y} \overset{⃑}{e_{x''}} + \sin θ_{y} \overset{⃑}{e_{z''}}) + Y_{0}^{'} \overset{⃑}{e_{y''}} + Z_{0}^{'} (- \sin θ_{y} \overset{⃑}{e_{x''}} + \cos θ_{y} \overset{⃑}{e_{z''}})$

　　＝ $(X_{0}^{'} \cos θ_{y} - Z_{0}^{'} \sin θ_{y}) \overset{⃑}{e_{x''}} + Y_{0}^{'} \overset{⃑}{e_{y''}} + (X_{0}^{'} {s i n θ}_{y} + Z_{0}^{'} {c o s θ}_{y}) \overset{⃑}{e_{z''}}$

　　＝ $X_{0}^{''} \overset{⃑}{e_{x''}} + Y_{0}^{''} \overset{⃑}{e_{y''}} + Z_{0}^{''} \overset{⃑}{e_{z''}}$ 式(12-8)

従って

$\begin{matrix} X_{0}^{''} = X_{0}^{'} \cos θ_{y} - Z_{0}^{'} \sin θ_{y} \\ Y_{0}^{''} = Y_{0}^{'} \\ Z_{0}^{''} = X_{0}^{'} {s i n θ}_{y} + Z_{0}^{'} {c o s θ}_{y} \end{matrix}\}$ 式(12-9)

逆に解くと

$\begin{matrix} X_{0}^{'} = X_{0}^{''} \cos θ_{y} + Z_{0}^{''} \sin θ_{y} \\ Y_{0}^{'} = Y_{0}^{''} \\ Z_{0}^{'} = {- X}_{0}^{''} {s i n θ}_{y} + Z_{0}^{''} {c o s θ}_{y} \end{matrix}\}$ 式(12-10)

式(12-6)で　 $\overset{⃑}{e_{x'}}, \overset{⃑}{e_{y'}}, \overset{⃑}{e_{z'}}$ 　を　式（12-1)を用いて $\overset{⃑}{e_{x}}, \overset{⃑}{e_{y}}, \overset{⃑}{e_{z}}$ 　で表すと

$\begin{matrix} \overset{⃑}{e_{x''}} = \cos θ_{y} \overset{⃑}{e_{x}} - \sin θ_{y} (- \sin θ_{x} \overset{⃑}{e_{y}} + \cos θ_{x} \overset{⃑}{e_{z}}) \\ = \cos θ_{y} \overset{⃑}{e_{x}} + \sin θ_{y} \sin θ_{x} \overset{⃑}{e_{y}} - \sin θ_{y} \cos θ_{x} \overset{⃑}{e_{z}} \\ \overset{⃑}{e_{y''}} = \cos θ_{x} \overset{⃑}{e_{y}} + \sin θ_{x} \overset{⃑}{e_{z}} \\ \overset{⃑}{e_{z^{''}}} = \sin θ_{y} \overset{⃑}{e_{x}} + \cos θ_{y} (- \sin θ_{x} \overset{⃑}{e_{y}} + \cos θ_{x} \overset{⃑}{e_{z}}) \\ = \sin θ_{y} \overset{⃑}{e_{x}} - \cos θ_{y} \sin θ_{x} \overset{⃑}{e_{y}} + \cos θ_{y} \cos θ_{x} \overset{⃑}{e_{z}} \end{matrix}\}$ 式(12-11)

また、点Pの座標の式（12-3)は式（12-7)を用いて

$\overset{⃑}{O P}$ $= X_{0} (\cos θ_{y} \overset{⃑}{e_{x''}} + \sin θ_{y} \overset{⃑}{e_{z''}})$

　　 $+ (Y_{0} {c o s θ}_{x} + Z_{0} {s i n θ}_{x}) \overset{⃑}{e_{y''}} + ({- Y}_{0} {s i n θ}_{x} + Z_{0} {c o s θ}_{x}) (- \sin θ_{y} \overset{⃑}{e_{x''}} + \cos θ_{y} \overset{⃑}{e_{z''}})$

　　＝ $\{X_{0} \cos θ_{y} - ({- Y}_{0} {s i n θ}_{x} + Z_{0} {c o s θ}_{x}) \sin θ_{y}\} \overset{⃑}{e_{x''}}$ $+ (Y_{0} {c o s θ}_{x} + Z_{0} {s i n θ}_{x}) \overset{⃑}{e_{y''}}$

$＋ \{X_{0} \sin θ_{y} + ({- Y}_{0} {s i n θ}_{x} + Z_{0} {c o s θ}_{x}) \cos θ_{y}\} \overset{⃑}{e_{z''}}$ 式(12-13)

最後に $Z "$ 軸の周りに $θ_{z}$ 回転させるとFig.20　より

$\begin{matrix} \overset{⃑}{e_{x'''}} = \cos θ_{z} \overset{⃑}{e_{x''}} + \sin θ_{z} \overset{⃑}{e_{y''}} \\ \overset{⃑}{e_{y'''}} = - \sin θ_{z} \overset{⃑}{e_{x''}} + \cos θ_{z} \overset{⃑}{e_{y''}} \\ \overset{⃑}{e_{z^{'''}}} = \overset{⃑}{e_{z''}} \end{matrix}\}$ 式(12-14)

式（12-14)を $\overset{⃑}{e_{x''}}, \overset{⃑}{e_{y''}}, \overset{⃑}{e_{z''}}$ について解くと

$\begin{matrix} \overset{⃑}{e_{x''}} = \cos θ_{z} \overset{⃑}{e_{x'''}} - \sin θ_{z} \overset{⃑}{e_{y'''}} \\ \overset{⃑}{e_{y''}} = \sin θ_{z} \overset{⃑}{e_{x'''}} + \cos θ_{z} \overset{⃑}{e_{y'''}} \\ \overset{⃑}{e_{z''}} = \overset{⃑}{e_{z'''}} \end{matrix}\}$ 式(12-15)

また、Pの座標はXYZ座標系で $(X_{0}^{'''}, Y_{0}^{'''}, Z_{0}^{'''})$ と表せるので式（12-15）を用いて

$\overset{⃑}{O P}$ ＝ $X_{0}^{''} \overset{⃑}{e_{x''}} + Y_{0}^{''} \overset{⃑}{e_{y''}} + Z_{0}^{''} \overset{⃑}{e_{z''}}$

　　＝ $X_{0}^{''} (\cos θ_{z} \overset{⃑}{e_{x'''}} - \sin θ_{z} \overset{⃑}{e_{y'''}}) + Y_{0}^{''} (\sin θ_{z} \overset{⃑}{e_{x'''}} + \cos θ_{z} \overset{⃑}{e_{y'''}}) + Z_{0}^{''} \overset{⃑}{e_{z'''}}$

　　＝ $(X_{0}^{''} \cos θ_{z} + Y_{0}^{''} \sin θ_{z}) \overset{⃑}{e_{x^{'''}}} + ({- X}_{0}^{''} {s i n θ}_{z} + Y_{0}^{''} {c o s θ}_{z}) \overset{⃑}{e_{y^{'''}}} + Z_{0}^{''} \overset{⃑}{e_{z^{'''}}}$

　　＝ $X_{0}^{'''} \overset{⃑}{e_{x'''}} + Y_{0}^{'''} \overset{⃑}{e_{y'''}} + Z_{0}^{'''} \overset{⃑}{e_{z'''}}$ 式(12-16)

従って

$\begin{matrix} X_{0}^{'''} = X_{0}^{''} \cos θ_{z} + Y_{0}^{''} \sin θ_{z} \\ Y_{0}^{'''} = - X_{0}^{''} \sin θ_{z} + Y_{0}^{''} \cos θ_{z} \\ Z_{0}^{'''} = Z_{0}^{''} \end{matrix}\}$ 式(12-17)

逆に解くと

$\begin{matrix} X_{0}^{''} = X_{0}^{'''} \cos θ_{z} - Y_{0}^{'''} \sin θ_{z} \\ Y_{0}^{''} = X_{0}^{'''} \sin θ_{z} + Y_{0}^{'''} \cos θ_{z} \\ Z_{0}^{''} = Z_{0}^{'''} \end{matrix}\}$ 式(12-18)

また式（12-14)は、 $\overset{⃑}{e_{x''}}, \overset{⃑}{e_{y''}}, \overset{⃑}{e_{z''}}$ について式(12-11)を用いると　

$\begin{matrix} \overset{⃑}{e_{x^{'''}}} = \cos θ_{z} (\cos θ_{y} \overset{⃑}{e_{x}} + \sin θ_{y} \sin θ_{x} \overset{⃑}{e_{y}} - \sin θ_{y} \cos θ_{x} \overset{⃑}{e_{z}}) \\ + \sin θ_{z} (\cos θ_{x} \overset{⃑}{e_{y}} + \sin θ_{x} \overset{⃑}{e_{z}}) \\ = \cos θ_{z} \cos θ_{y} \overset{⃑}{e_{x}} + (\cos θ_{z} \sin θ_{y} \sin θ_{x} + \sin θ_{z} \cos θ_{x}) \overset{⃑}{e_{y}} \\ + (- \cos θ_{z} \sin θ_{y} \cos θ_{x} + \sin θ_{z} \sin θ_{x}) \overset{⃑}{e_{z}} \\ \overset{⃑}{e_{y^{'''}}} = - \sin θ_{z} (\cos θ_{y} \overset{⃑}{e_{x}} + \sin θ_{y} \sin θ_{x} \overset{⃑}{e_{y}} - \sin θ_{y} \cos θ_{x} \overset{⃑}{e_{z}}) \\ + \cos θ_{z} (\cos θ_{x} \overset{⃑}{e_{y}} + \sin θ_{x} \overset{⃑}{e_{z}}) \\ = - \sin θ_{z} \cos θ_{y} \overset{⃑}{e_{x}} + (- \sin θ_{z} \sin θ_{y} \sin θ_{x} + \cos θ_{z} \cos θ_{x}) \overset{⃑}{e_{y}} \\ + (\sin θ_{z} \sin θ_{y} \cos θ_{x} + \cos θ_{z} \sin θ_{x}) \overset{⃑}{e_{z}} \\ \overset{⃑}{e_{z^{'''}}} = \sin θ_{y} \overset{⃑}{e_{x}} - \cos θ_{y} \sin θ_{x} \overset{⃑}{e_{y}} + \cos θ_{y} \cos θ_{x} \overset{⃑}{e_{z}} \end{matrix}\}$ 式(12-19)

式（12-19)を逆に $\overset{⃑}{e_{x}}, \overset{⃑}{e_{y}}, \overset{⃑}{e_{z}}$ 　について解く。その時式（12-2) , 式（12-7) , 式（12-15)を用いる。

$\begin{matrix} \overset{⃑}{e_{x}} = \overset{⃑}{e_{x'}} = \cos θ_{y} \overset{⃑}{e_{x''}} + \sin θ_{y} \overset{⃑}{e_{z''}} \\ = \cos θ_{y} (\cos θ_{z} \overset{⃑}{e_{x'''}} - \sin θ_{z} \overset{⃑}{e_{y'''}}) + \sin θ_{y} \overset{⃑}{e_{z'''}} \\ = \cos θ_{y} \cos θ_{z} \overset{⃑}{e_{x'''}} - \cos θ_{y} \sin θ_{z} \overset{⃑}{e_{y'''}} + \sin θ_{y} \overset{⃑}{e_{z'''}} \\ \overset{⃑}{e_{y}} = \cos θ_{x} \overset{⃑}{e_{y'}} - \sin θ_{x} \overset{⃑}{e_{z'}} \\ = \cos θ_{x} \overset{⃑}{e_{y^{''}}} - \sin θ_{x} (- \sin θ_{y} \overset{⃑}{e_{x^{''}}} + \cos θ_{y} \overset{⃑}{e_{z^{''}}}) \\ = \cos θ_{x} (\sin θ_{z} \overset{⃑}{e_{x'''}} + \cos θ_{z} \overset{⃑}{e_{y'''}}) \\ - \sin θ_{x} \{- \sin θ_{y} (\cos θ_{z} \overset{⃑}{e_{x'''}} - \sin θ_{z} \overset{⃑}{e_{y'''}}) + \cos θ_{y} \overset{⃑}{e_{z'''}}\} \\ = (\cos θ_{x} \sin θ_{z} + \sin θ_{x} \sin θ_{y} \cos θ_{z}) \overset{⃑}{e_{x^{'''}}} \\ + (\cos θ_{x} \cos θ_{z} - \sin θ_{x} \sin θ_{y} \sin θ_{z}) \overset{⃑}{e_{y^{'''}}} - \sin θ_{x} \cos θ_{y} \overset{⃑}{e_{z'''}} \\ \overset{⃑}{e_{z}} = \sin θ_{x} \overset{⃑}{e_{y^{'}}} + \cos θ_{x} \overset{⃑}{e_{z^{'}}} \\ = \sin θ_{x} \overset{⃑}{e_{y^{''}}} + \cos θ_{x} (- \sin θ_{y} \overset{⃑}{e_{x^{''}}} + \cos θ_{y} \overset{⃑}{e_{z^{''}}}) \\ = \sin θ_{x} (\sin θ_{z} \overset{⃑}{e_{x^{'''}}} + \cos θ_{z} \overset{⃑}{e_{y^{'''}}}) \\ + \cos θ_{x} \{- \sin θ_{y} (\cos θ_{z} \overset{⃑}{e_{x^{'''}}} - \sin θ_{z} \overset{⃑}{e_{y^{'''}}}) + \cos θ_{y} \overset{⃑}{e_{z^{'''}}}\} \\ = (\sin θ_{x} \sin θ_{z} - \cos θ_{x} \sin θ_{y} \cos θ_{z}) \overset{⃑}{e_{x^{'''}}} \\ + (\sin θ_{x} \cos θ_{z} + \cos θ_{x} \sin θ_{y} \sin θ_{z}) \overset{⃑}{e_{y^{'''}}} + \cos θ_{x} \cos θ_{y} \overset{⃑}{e_{z'''}} \end{matrix}\}$ 式(12-20)

式（12-13)は式（12-15)を用いると

$\overset{⃑}{O P}$

＝ $\{X_{0} \cos θ_{y} - ({- Y}_{0} {s i n θ}_{x} + Z_{0} {c o s θ}_{x}) \sin θ_{y}\} (\cos θ_{z} \overset{⃑}{e_{x^{'''}}} - \sin θ_{z} \overset{⃑}{e_{y^{'''}}})$

$+ (Y_{0} {c o s θ}_{x} + Z_{0} {s i n θ}_{x}) (\sin θ_{z} \overset{⃑}{e_{x'''}} + \cos θ_{z} \overset{⃑}{e_{y'''}})$

$＋ \{X_{0} \sin θ_{y} + ({- Y}_{0} {s i n θ}_{x} + Z_{0} {c o s θ}_{x}) \cos θ_{y}\} \overset{⃑}{e_{z'''}}$

$= [\{X_{0} \cos θ_{y} - ({- Y}_{0} {s i n θ}_{x} + Z_{0} {c o s θ}_{x}) \sin θ_{y}\} \cos θ_{z} + (Y_{0} {c o s θ}_{x} + Z_{0} {s i n θ}_{x}) \sin θ_{z}] \overset{⃑}{e_{x^{'''}}}$

$+ [- \{X_{0} \cos θ_{y} - ({- Y}_{0} {s i n θ}_{x} + Z_{0} {c o s θ}_{x}) \sin θ_{y}\} \sin θ_{z} + (Y_{0} {c o s θ}_{x} + Z_{0} {s i n θ}_{x}) \cos θ_{z}] \overset{⃑}{e_{y'''}}$

$＋ \{X_{0} \sin θ_{y} + ({- Y}_{0} {s i n θ}_{x} + Z_{0} {c o s θ}_{x}) \cos θ_{y}\} \overset{⃑}{e_{z'''}}$ 式(12-21)

となる。

--------磁石専用磁場計算アプリケーション(Kojimag)に興味がある方はこちらへ--------

このサイトの基礎計算式を基に磁石専用アプリケーションを開発しました。
こちらから”磁石専用磁場計算アプリケーション(Kojimag)”からKojimagの詳細について確認できます。