§１２．全体座標系と固有座標系３）座標系の平行移動

§１２．全体座標系と固有座標系

３）座標系の平行移動

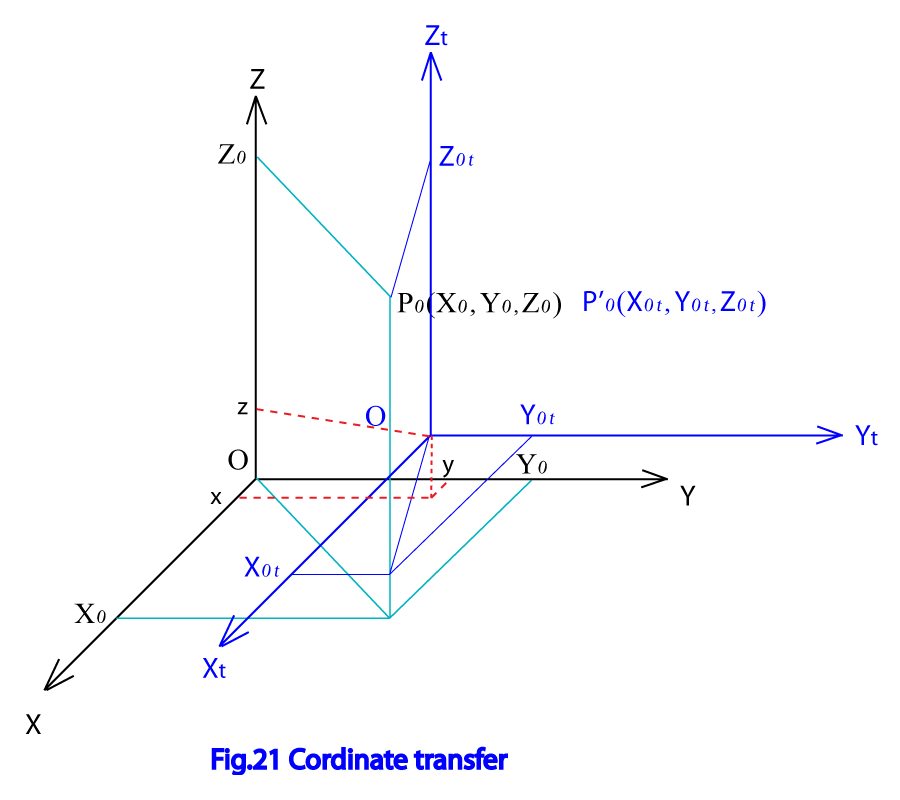
　Fig.21に示したように全体座標系XYZ をベクトル量　 $(x, y, z)$ 　平行移動した座標系 $X t Y t Z t$ 　を考える。XYZ座標系の点 $P_{0} (X_{0}, Y_{0}, Z_{0})$ 　は $X t Y t Z t$ 　座標系で　 $P_{0 t} (X_{0 t}, Y_{0 t}, Z_{0 t})$ 　と表せるとする。

X,Y,Z座標系の平行移動

$X_{0 t} = X_{0} - x, Y_{0 t} = Y_{0} - y, Z_{0 t} = Z_{0} - z$ 式(12-35)

またXt Yt Zt軸の単位ベクトル $\overset{⃑}{e_{x_{t}}}, \overset{⃑}{e_{y_{t}}}, \overset{⃑}{e_{z_{t}}}$ 　は

$\begin{matrix} \overset{⃑}{e_{x_{t}}} = \overset{⃑}{e_{x}} \\ \overset{⃑}{e_{y_{t}}} = \overset{⃑}{e_{y}} \\ \overset{⃑}{e_{z_{t}}} = \overset{⃑}{e_{z}} \end{matrix}\}$ 式(12-36)

が成り立つ。これは行列表記では

$(X_{0 t}, Y_{0 t}, Z_{0 t}, 1) = (X_{0}, Y_{0}, Z_{0}, 1) (\begin{matrix} 1 \\ 0 \\ 0 \\ - x \end{matrix} \begin{matrix} 0 \\ 1 \\ 0 \\ - y \end{matrix} \begin{matrix} 0 \\ 0 \\ 1 \\ - z \end{matrix} \begin{matrix} 0 \\ 0 \\ 0 \\ 1 \end{matrix})$ 式(12-37)

となる。

逆に、ローカル座標系から全体座標系への変換式は　式(12-37)　を逆に解いて

$(X_{0}, Y_{0}, Z_{0}, 1) = (X_{0 t}, Y_{0 t}, Z_{0 t}, 1) (\begin{matrix} 1 \\ 0 \\ 0 \\ x \end{matrix} \begin{matrix} 0 \\ 1 \\ 0 \\ y \end{matrix} \begin{matrix} 0 \\ 0 \\ 1 \\ z \end{matrix} \begin{matrix} 0 \\ 0 \\ 0 \\ 1 \end{matrix})$ 式(12-37')

--------磁石専用磁場計算アプリケーション(Kojimag)に興味がある方はこちらへ--------

このサイトの基礎計算式を基に磁石専用アプリケーションを開発しました。
こちらから”磁石専用磁場計算アプリケーション(Kojimag)”からKojimagの詳細について確認できます。