§１７．磁石に働く力の計算３）一般角柱磁石に働く力の計算

§１７．磁石に働く力の計算

３）一般角柱磁石に働く力の計算

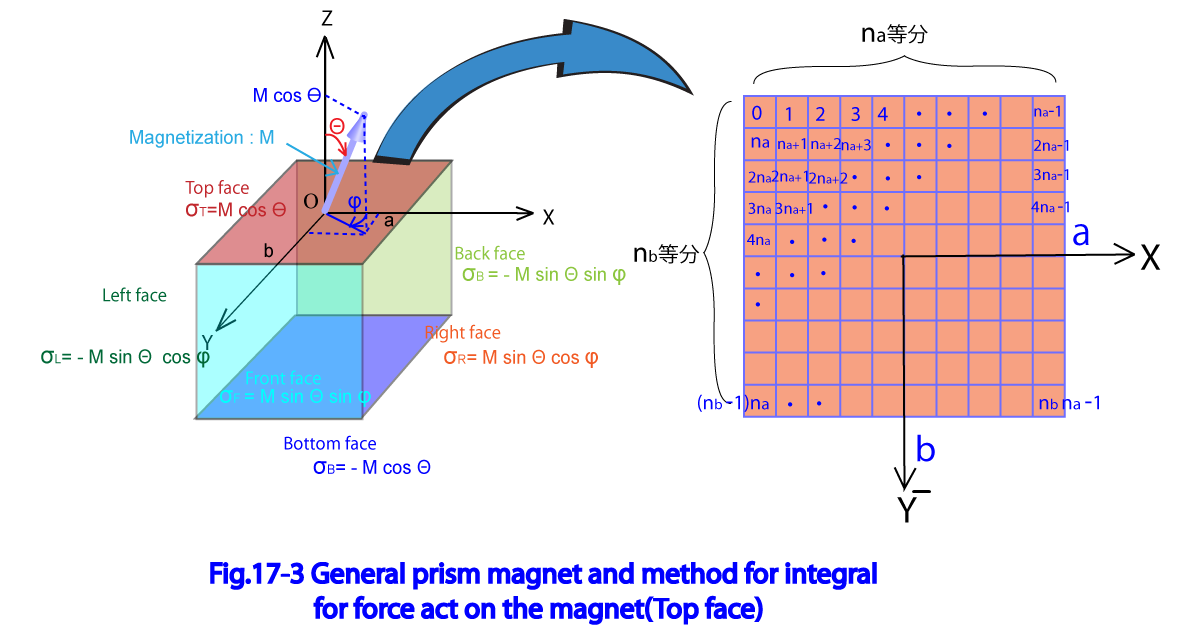
一般角柱磁石に働く力（上面）

　§１７-２）では、磁化がＺ軸方向を向いた磁石に働く力を考察した。ここでは磁化が任意の方向を向く事ができる一般角柱磁石を考察する。　一般角柱磁石は§１４で定義されている。（左手系で考える。）

1)上面の磁荷による力への寄与

Fig17-3に一般角柱磁石の定義と、上面の積分面を示している。　　 X軸を $n_{a}$ 等分、Y軸を　 $n_{b}$ 等分すると仮定し、X軸方向に i番目の列 $(i = 0,1, 2 \dots)$ 　Y軸方向にj番目の行 $(j = 0,1, 2 \dots)$ となる格子 $(i, j)$ の中心座標 $(X_{i}, Y_{j}, Z_{i, j})$ は一般角柱磁石のローカル座標系を用いて

$X_{i} = - a + \frac{a}{n_{a}} ∙ (2 i + 1),$ $Y_{j} = - b + \frac{b}{n_{b}} ∙ (2 j + 1),$ $Z_{i, j} = 0$ 式(17-9)

と表すことができる。従ってこの微小格子要素面　 $(i, j)$ 　に働く力　 ${\overset{⃑}{F}}_{T o p X} (i, j)$ は

${\overset{⃑}{F}}_{T o p} (i, j) = σ_{T} ∙ 2 a / n_{a} ∙ 2 b / n_{b} ∙ \overset{⃑}{H} (X_{i}, Y_{j}, 0)$ 式(17-10)

と表すことができる。上面すべての格子面に働く力は　 $σ_{T} = M \cos Θ$ を用いて

${\overset{⃑}{F}}_{T o p} = M \cos Θ ∙ 4 a b / (n_{a} n_{b}) \sum_{i = 0}^{n_{a} - 1} \sum_{j = 0}^{n_{b} - 1} \overset{⃑}{H} (X_{i}, Y_{j}, 0)$ 式(17-11)

により表すことができる。

2)右側面の磁荷による力への寄与

Fig17-4に一般角柱磁石の定義と、右側面の積分面を示している。

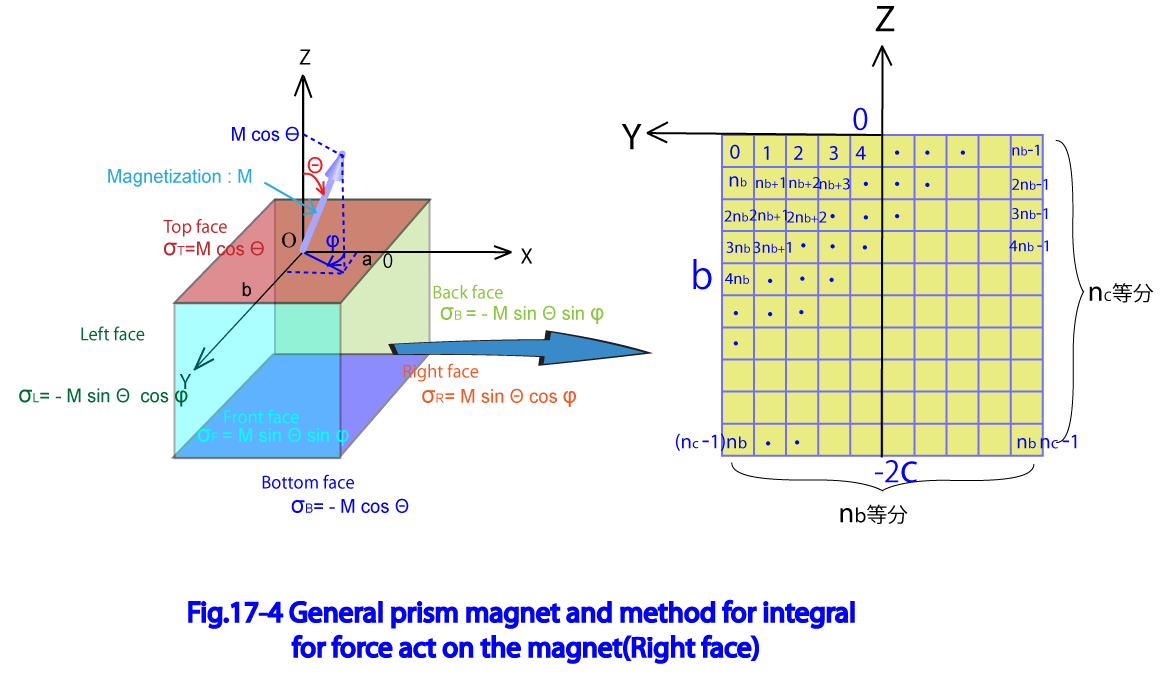
一般角柱磁石に働く力（右側面）

　 Y軸を $n_{b}$ 等分、Z軸を　 $n_{c}$ 等分すると仮定し、Y軸方向に i番目の列 $(i = 0,1, 2 \dots)$ 　Z軸方向にj番目の行 $(j = 0,1, 2 \dots)$ となる格子 $(i, j)$ の中心座標 $(X_{i, j}, Y_{j}, Z_{j})$ は一般角柱磁石のローカル座標系を用いて

$X_{i, j} = a,$ $Y_{i} = b - \frac{b}{n_{b}} ∙ (2 i + 1),$ $Z_{j} = - \frac{c}{n_{c}} ∙ (2 j + 1)$ 式(17-12)

と表すことができる。従ってこの微小格子要素面　 $(i, j)$ 　に働く力　 ${\overset{⃑}{F}}_{R i g h t} (i, j)$ は

${\overset{⃑}{F}}_{R i g h t} (i, j) = σ_{R} ∙ 2 b / n_{b} ∙ 2 c / n_{c} ∙ \overset{⃑}{H} (a, Y_{i}, Z_{j})$ 式(17-13)

と表すことができる。上面すべての格子面に働く力は　 $σ_{R} = M \sin Θ \cos Ψ$ を用いて

${\overset{⃑}{F}}_{R i g h t} = M \sin Θ \cos Ψ ∙ 4 b c / (n_{b} n_{c}) \sum_{i = 0}^{n_{b} - 1} \sum_{j = 0}^{n_{c} - 1} \overset{⃑}{H} (a, Y_{i}, Z_{j})$ 式(17-14)

により表すことができる。

3)前面の磁荷による力への寄与

　Fig17-5に一般角柱磁石の定義と、前面の積分面を示している。

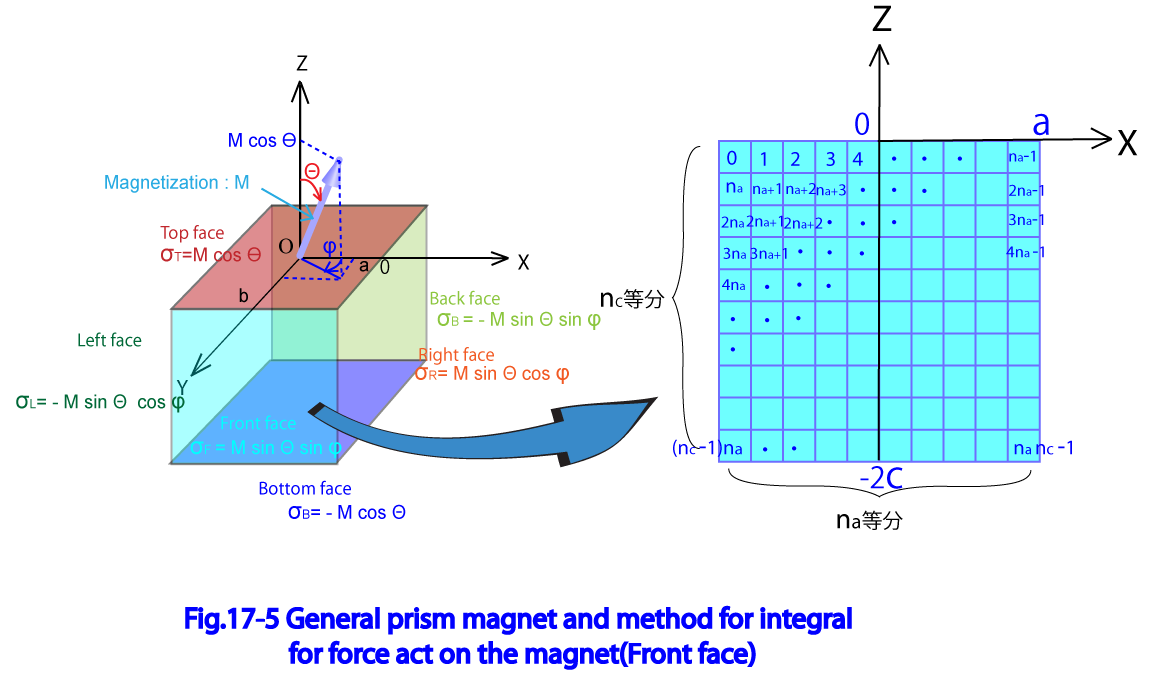
一般角柱磁石に働く力（前面）

X軸を $n_{a}$ 等分、Z軸を　 $n_{c}$ 等分すると仮定し、X軸方向に i番目の列 $(i = 0,1, 2 \dots)$ 　Z軸方向にj番目の行 $(j = 0,1, 2 \dots)$ となる格子 $(i, j)$ の中心座標 $(X_{i}, Y_{i, j}, Z_{j})$ は一般角柱磁石のローカル座標系を用いて

$X_{i} = - a + \frac{a}{n_{a}} ∙ (2 i + 1),$ $Y_{i, j} = b,$ $Z_{j} = - \frac{c}{n_{c}} ∙ (2 j + 1)$ 式(17-15)

と表すことができる。従ってこの微小格子要素面　 $(i, j)$ 　に働く力　 ${\overset{⃑}{F}}_{F r o n t} (i, j)$ は

${\overset{⃑}{F}}_{F r o n t} (i, j) = σ_{F} ∙ 2 a / n_{a} ∙ 2 c / n_{c} ∙ \overset{⃑}{H} (X_{i}, b, Z_{j})$ 式(17-16)

と表すことができる。上面すべての格子面に働く力は　 $σ_{F} = M \sin Θ \sin Ψ$ を用いて

${\overset{⃑}{F}}_{F r o n t} = M \sin Θ \sin Ψ ∙ 4 a c / (n_{a} n_{c}) \sum_{i = 0}^{n_{a} - 1} \sum_{j = 0}^{n_{c} - 1} \overset{⃑}{H} (X_{i}, b, Z_{j})$ 式(17-17)

により表すことができる。

4)左側面の磁荷による力への寄与

Fig17-6に一般角柱磁石の定義と、左側面の積分面を示している。

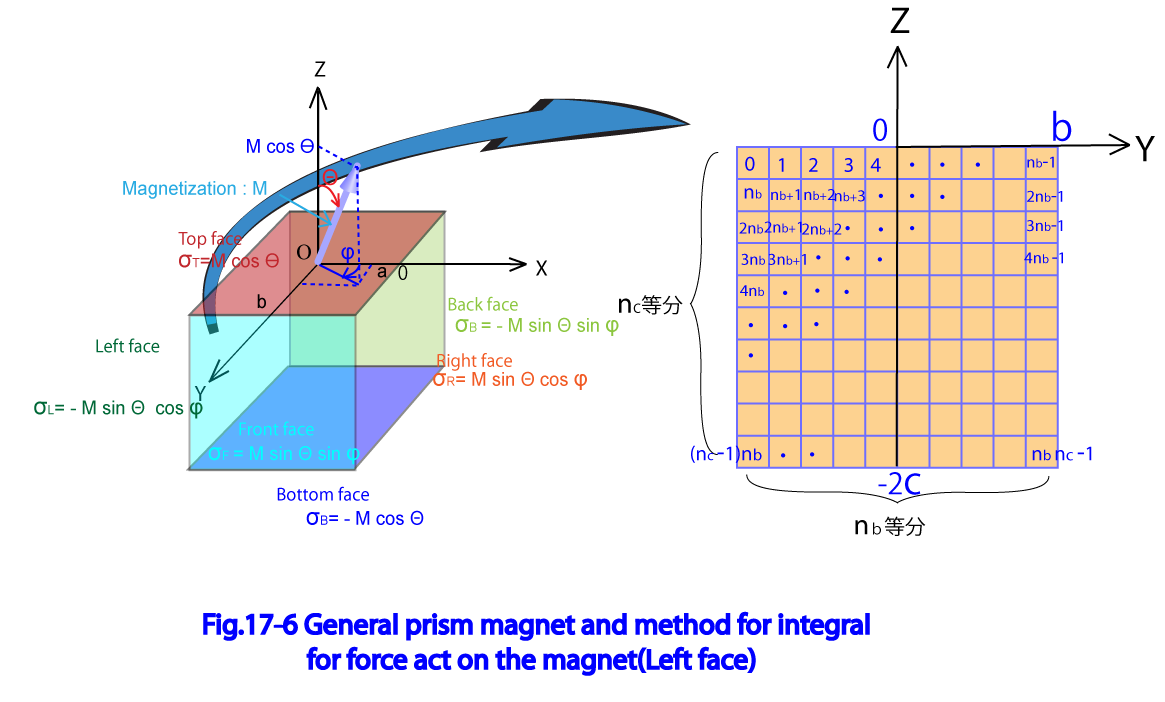
一般角柱磁石に働く力（左側面面）

　　 Y軸を $n_{b}$ 等分、Z軸を　 $n_{c}$ 等分すると仮定し、Y軸方向に i番目の列 $(i = 0,1, 2 \dots)$ 　Z軸方向にj番目の行 $(j = 0,1, 2 \dots)$ となる格子 $(i, j)$ の中心座標 $(X_{i, j}, Y_{i}, Z_{j})$ は一般角柱磁石のローカル座標系を用いて

$X_{i, j} = - a,$ $Y_{i} = - b + \frac{b}{n_{b}} ∙ (2 i + 1),$ $Z_{j} = - \frac{c}{n_{c}} ∙ (2 j + 1)$ 式(17-18)

と表すことができる。従ってこの微小格子要素面　 $(i, j)$ 　に働く力　 ${\overset{⃑}{F}}_{L e f t} (i, j)$ は

${\overset{⃑}{F}}_{L e f t} (i, j) = σ_{L} ∙ 2 b / n_{b} ∙ 2 c / n_{c} ∙ \overset{⃑}{H} (- a, Y_{i}, Z_{j})$ 式(17-19)

と表すことができる。上面すべての格子面に働く力は　 $σ_{L} = - M \sin Θ \cos Ψ$ を用いて

${\overset{⃑}{F}}_{L e f t} = - M \sin Θ \cos Ψ ∙ 4 b c / (n_{b} n_{c}) \sum_{i = 0}^{n_{b} - 1} \sum_{j = 0}^{n_{c} - 1} \overset{⃑}{H} (- a, Y_{i}, Z_{j})$ 式(17-20)

により表すことができる。

5)背面の磁荷による力への寄与

　Fig17-7に一般角柱磁石の定義と、背面の積分面を示している。

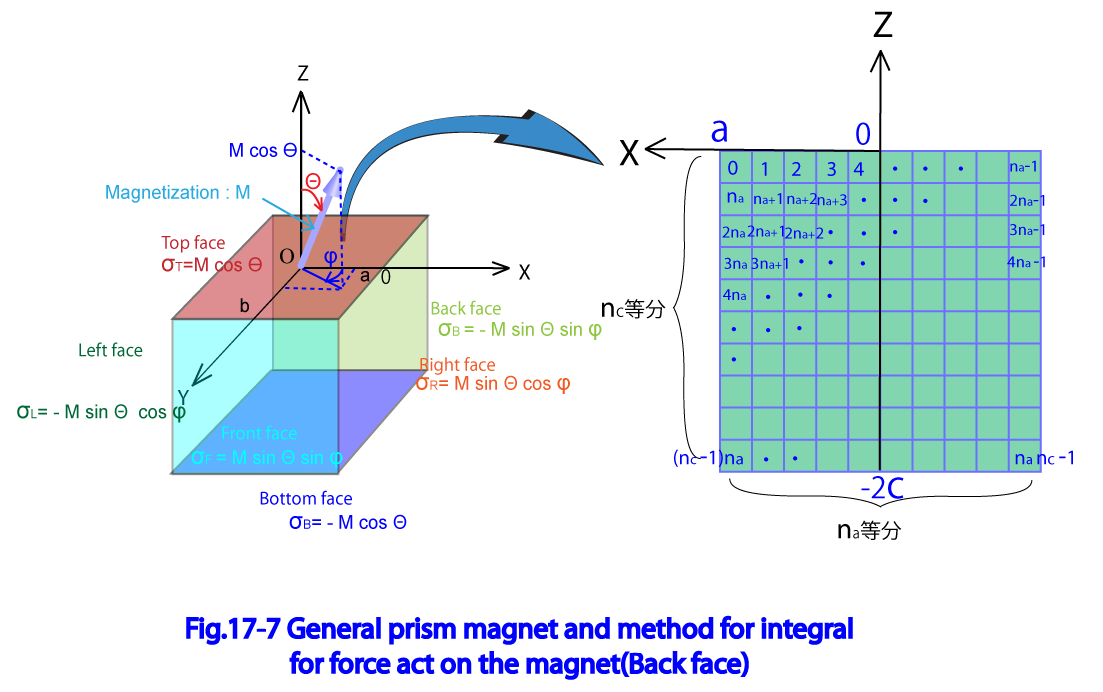
一般角柱磁石に働く力（背面）

X軸を $n_{a}$ 等分、Z軸を　 $n_{c}$ 　等分すると仮定し、X軸方向に i番目の列 $(i = 0,1, 2 \dots)$ 　Z軸方向にj番目の行 $(j = 0,1, 2 \dots)$ となる格子 $(i, j)$ の中心座標 $(X_{i}, Y_{i, j}, Z_{j})$ は一般角柱磁石のローカル座標系を用いて

$X_{i} = a - \frac{a}{n_{a}} ∙ (2 i + 1),$ $Y_{i, j} = - b,$ $Z_{j} = - \frac{c}{n_{c}} ∙ (2 j + 1)$ 式(17-21)

と表すことができる。従ってこの微小格子要素面　 $(i, j)$ 　に働く力　 ${\overset{⃑}{F}}_{B a c k} (i, j)$ は

${\overset{⃑}{F}}_{B a c k} (i, j) = σ_{B} ∙ 2 a / n_{a} ∙ 2 c / n_{c} ∙ \overset{⃑}{H} (X_{i}, - b, Z_{j})$ 式(17-22)

と表すことができる。上面すべての格子面に働く力は　 $σ_{B} = - M \sin Θ \sin Ψ$ を用いて

${\overset{⃑}{F}}_{B a c k} = - M \sin Θ \sin Ψ ∙ 4 a c / (n_{a} n_{c}) \sum_{i = 0}^{n_{a} - 1} \sum_{j = 0}^{n_{c} - 1} \overset{⃑}{H} (X_{i}, - b, Z_{j})$ 式(17-23)

により表すことができる。

6)底面の磁荷による力への寄与

　Fig17-8に一般角柱磁石の定義と、底面の積分面を示している。

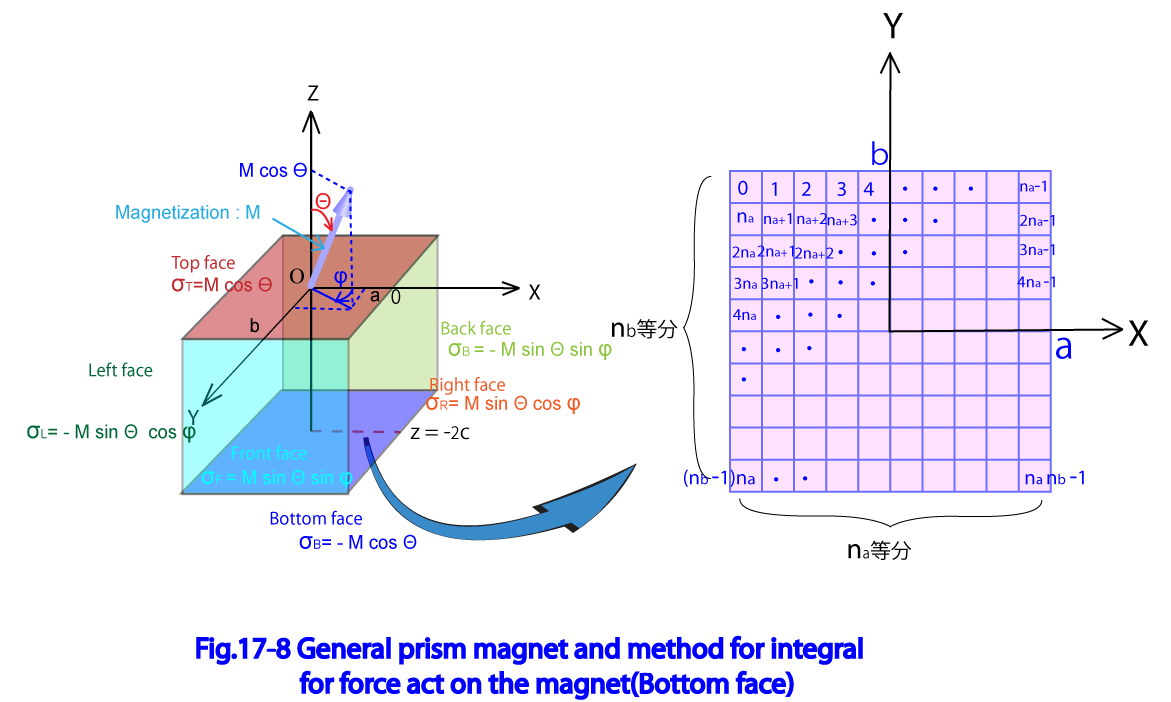
一般角柱磁石に働く力（底面）

X軸を $n_{a}$ 等分、Y軸を　 $n_{b}$ 等分すると仮定し、X軸方向に i番目の列 $(i = 0,1, 2 \dots)$ 　Y軸方向にj番目の行 $(j = 0,1, 2 \dots)$ となる格子 $(i, j)$ の中心座標 $(X_{i}, Y_{j}, Z_{i, j})$ は一般角柱磁石のローカル座標系を用いて

$X_{i} = - a + \frac{a}{n_{a}} ∙ (2 i + 1),$ $Y_{j} = b - \frac{b}{n_{b}} ∙ (2 j + 1),$ $Z_{i, j} = - 2 c$ 式(17-24)

と表すことができる従ってこの微小格子要素面　 $(i, j)$ 　に働く力　 ${\overset{⃑}{F}}_{B o t t o m} (i, j)$ ) は

${\overset{⃑}{F}}_{B o t t o m} (i, j) = σ_{B} ∙ 2 a / n_{a} ∙ 2 b / n_{b} ∙ \overset{⃑}{H} (X_{i}, Y_{j}, - 2 c)$ 式(17-25)

と表すことができる。上面すべての格子面に働く力は　 $σ_{B} = - M \cos Θ$ を用いて

${\overset{⃑}{F}}_{B o t t o m} = - M \cos Θ ∙ 4 a b / (n_{a} n_{b}) \sum_{i = 0}^{n_{a} - 1} \sum_{j = 0}^{n_{b} - 1} \overset{⃑}{H} (X_{i}, Y_{j}, - 2 c)$ 式(17-26)

により表すことができる。

--------磁石専用磁場計算アプリケーション(Kojimag)に興味がある方はこちらへ--------

このサイトの基礎計算式を基に磁石専用アプリケーションを開発しました。
こちらから”磁石専用磁場計算アプリケーション(Kojimag)”からKojimagの詳細について確認できます。

公開日：2013年5月6日　　　　　　更新日：2023年10月16日　　　　　
作成者：児島　伸生
連絡先：
2011-2023 Copyright by Kojimag