§１８．減磁曲線の温度依存性１）ネオジム磁石の場合

§１８．減磁曲線の温度依存性

3）不可逆熱減磁率の計算

各温度 Tにおける磁気特性は温度の関数で表すことができ、残留磁束密度については

$B_{r} (T) = B_{r 20} [1 + \frac{C_{b r}}{100} (T - 20)]$ 式(18-4)

と表すことができ、保磁力 $H_{c j}$ については

$H_{c j} (T) = H_{c j 20} [1 + \frac{C_{h c j}}{100} (T - 20)]$ 式(18-5)

と表すことができる。
次に、Fig.18-1で示された20℃における減磁曲線は、HとBの関数として、近似的に傾きが $μ_{r}$ で、点 $(0, B_{r 20})$ を通る直線で表すことができると考えられる。この直線を表す式は

$B = B_{r 20} + μ_{r} H$ 式(18-6)

と表すことができる。
Fig.18-1において、磁石のパーミアンスがPの時の20℃における動作点は $d_{20}$ で示されている。 $d_{20}$ は、パーミアンス線を表す直線の式

$B = - P H$ 式(18-7)

と　式(18-6)　との交点であるので、この2つの式から交点の座標を求めると

$(- \frac{B_{r 20}}{P + μ_{r}}, \frac{P B_{r 20}}{P + μ_{r}})$ 式(18-8)

となる。
次に100℃　における動作点　 $d_{100}$ を考える。例えば、Fig.18-1に示された代表的なネオジム磁石においては、温度上昇による保磁力 $H_{c j}$ の低下によりB-Hカーブに屈曲点（knee point）が生じ、この屈曲点を越えると急激に　B-Hカーブの落ち込みが発生する。動作点がこの屈曲点を越えると　Fig.18-1　の　 $d_{100}$ に示されているよう屈曲点がない場合の ${d'}_{100}$ より落ち込むことが分る。この落ち込みは、温度が20℃　に戻っても回復せず、加熱による不可逆減磁と呼ばれる。
この落ち込み量

$\frac{∆ B_{d}}{B_{d}} = \frac{B_{d' 100} - B_{d 100}}{B_{d' 100}}$ 式(18-9)

を表式化する。先ず100℃　における減磁曲線の直線部は、HとBの関数として、傾きが $μ_{r}$ で、点 $(0, B_{r 100})$ を通る直線で表すことができる。この直線部を表す式は

$B = B_{r 100} + μ_{r} H$ 式(18-10)

と表すことができる。式(18-8)を求めた時と同様に、これと式(18-7)との交点を求めることができ、

$(- \frac{B_{r 100}}{P + μ_{r}}, \frac{P B_{r 100}}{P + μ_{r}})$ 式(18-11)

すなわち

$B_{d' 100} = \frac{P B_{r 100}}{P + μ_{r}}$ 式(18-12)

と表せる。
Fig.18-2に100℃　における減磁曲線を再掲示した。ここでは、単純化の為、4πM-H曲線は屈曲点において直線で折れ曲がり、屈曲点から保磁力　 $H_{c j 100}$ 迄は直線で傾きが $μ_{m d}$ であると近似する。通常ネオジム磁石の場合この傾き　 $μ_{m d}$ 　は十分大きく40-50　Gauss/ Oe 程度となる。 $H_{c b 100}$ 0からの垂線が4πM-H曲線と交わる点を $m_{100}$ 　とすると　 $m_{100}$ 　の座標は

$(H_{c b 100}, - H_{c b 100})$ 式(18-13)

となり傾き　 $μ_{m d}$ 　は

$μ_{m d} = - H_{c b 100} / (H_{c b 100} - H_{c j 100})$ 式(18-14)

と表せる。

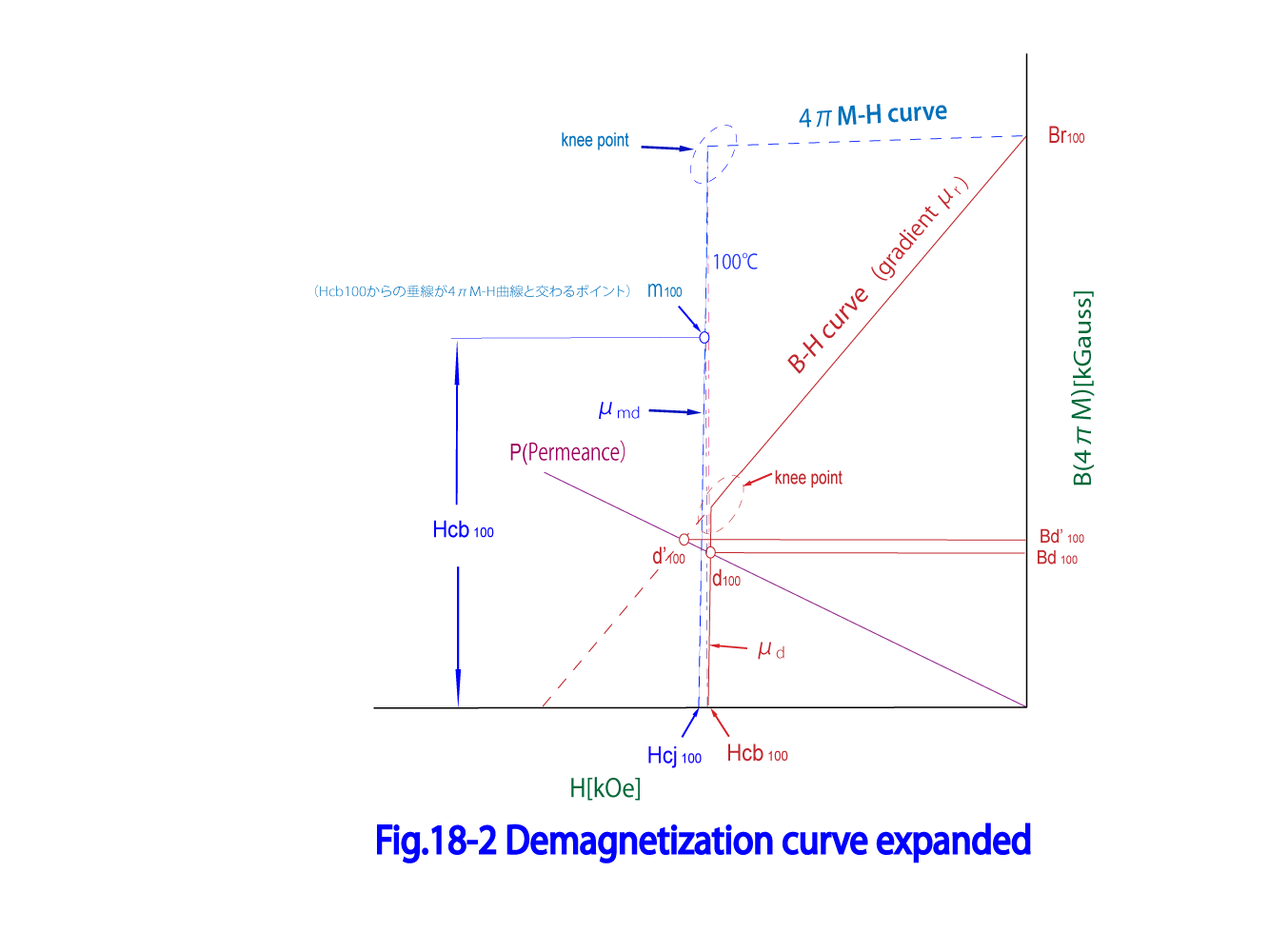
更に、B－H曲線の屈曲点以降の直線の傾きを $μ_{d}$ 　とすると $H_{c j 100}$ からの垂線がB-H曲線と交わる点は　 $H ＝ H_{c j 100}$ 　から　 ${- H}_{c j 100}$ だけB方向に下した点となるので

$μ_{d} = \frac{[{- H}_{c b 100} + (H_{c b 100} - H_{c j 100})]}{H_{c b 100} - H_{c j 100}} = μ_{m d} + 1$ 式(18-15)

となる事が判る。
これらより、100℃　におけるB-H減磁曲線において、傾きが　 $μ_{d}$ で表された落ち込み部分の直線を表す式は、 $(H_{c b 100}, 0)$ を通り傾きが　 $μ_{d}$ の直線になるので

$B = μ_{d} (H - H_{c b 100})$ 式(18-16)

と表すことができる。
次に100℃　における動作点　 $d_{100}$ 　の座標を式(18-16)と式(18-7)　より求める。

$(\frac{μ_{d} H_{c b 100}}{P + μ_{d}}, - \frac{P {μ_{d} H}_{c b 100}}{P + μ_{d}})$ 式(18-17)

すなわち

$B_{d 100} = - \frac{P {μ_{d} H}_{c b 100}}{P + μ_{d}}$ 式(18-18)

となる。式(18-9)で表された減磁率は式(18-12)、式(18-18)より求めることができ

$\frac{∆ B_{d}}{B_{d}} = \frac{B_{d^{'} 100} - B_{d 100}}{B_{d^{'} 100}}$

$= (\frac{P B_{r 100}}{P + μ_{r}} + \frac{P {μ_{d} H}_{c b 100}}{P + μ_{d}}) / (\frac{P B_{r 100}}{P + μ_{r}}) = (\frac{B_{r 100}}{1 + {P / μ}_{r}} + \frac{{μ_{r} H}_{c b 100}}{1 + P / μ_{d}}) / (\frac{B_{r 100}}{1 + {P / μ}_{r}})$ 式(18-19)

また、式(18-14)を $H_{c b 100}$ に関して解けば

$H_{c b 100} = H_{c j 100} / (1 + \frac{1}{μ_{m d}})$ 式(18-20)

となるので式(18-15)を用いれば、減磁率式(18-19)は　 $H_{c j 100}$ 　と $μ_{m d}$ を用いて表すことができる。

--------磁石専用磁場計算アプリケーション(Kojimag)に興味がある方はこちらへ--------

このサイトの基礎計算式を基に磁石専用アプリケーションを開発しました。
こちらから”磁石専用磁場計算アプリケーション(Kojimag)”からKojimagの詳細について確認できます。

公開日：2014年8月16日　　　　　　更新日：2023年10月16日　　　　　　
作成者：児島　伸生
連絡先：
2011-2023 Copyright by Kojimag