§2-2)チャージモデルの意味についての考察

§２．チャージモデルの考え方

2)チャージモデルの意味についての考察

磁場の表式(1-61)はMが一定の時式(1-59)の $ρ_{M} (x^{'}, y^{'}, z') \equiv - {\overset{⃑}{\nabla}}^{'} ∙ \overset{⃑}{M} (x^{'}, y^{'}, z') = 0$ となるので

$\overset{⃑}{B} (x, y, z) = \frac{μ_{0}}{4 π} \iint_{S_{0}}^{} σ_{M} (x^{'}, y^{'}, z') \frac{\overset{⃑}{R}}{R^{3}} {d A}^{'} ＋ μ_{0} \overset{⃑}{M} (x, y, z)$ 式(2-1)

と表す事ができる。これは、実際フェライト磁石、サマリウムコバルト磁石、ネオジム磁石等の微視的構造を調べた時構成粒子の磁化容易軸は、ほぼ一方向に揃っている事を考えればよい。

Fig.7に概念図を示した。

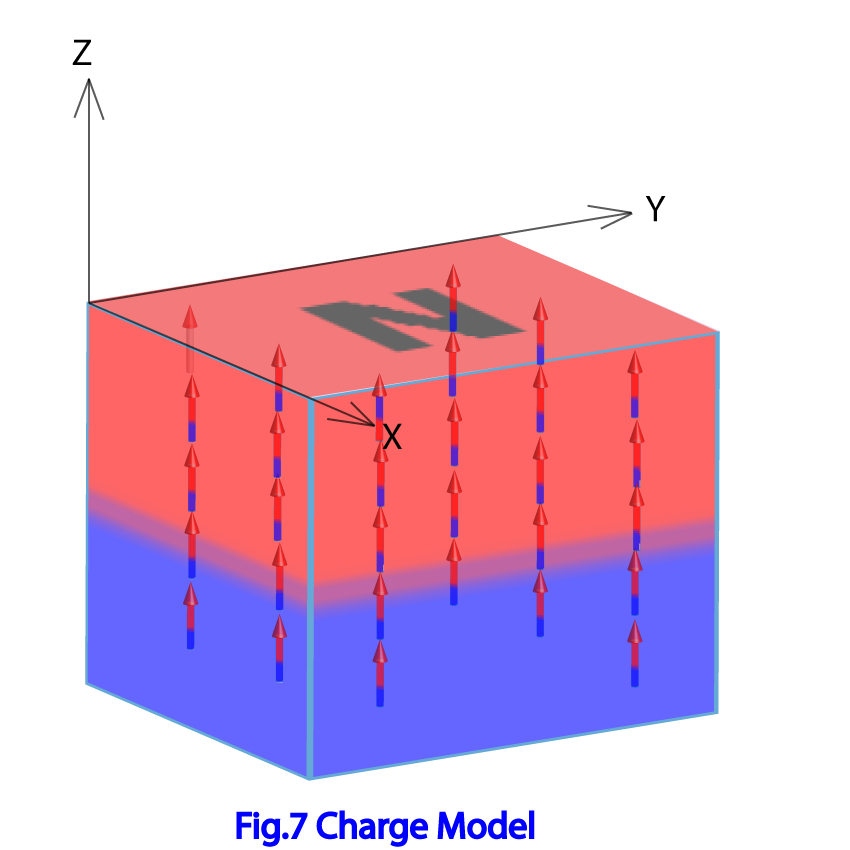
磁石内部にはZ軸方向を向いた一様な磁化Mが存在していると仮定する。磁石内部では、 $ρ_{M} (x^{'}, y^{'}, z') = 0$ を満足している為、磁場の発生源は無い。これは、上下に連なった磁化MのN極側とS極側が打ち消しあてゼロになると考えれば理解できる。磁石の上面には、式(2-1)の一項目に相当する表面磁極密度

$σ_{M} (x^{'}, y^{'}, z') \equiv \overset{⃑}{M} (x^{'}, y^{'}, z') ∙ \overset{⃑}{n} = B r$

がN極として磁場の発生源となって現れる。また、下面側には同様に

$σ_{M} (x^{'}, y^{'}, z') \equiv \overset{⃑}{M} (x^{'}, y^{'}, z') ∙ \overset{⃑}{n} = - B r$

がS極として磁場の発生源となって現れる。このように磁石の上下面であるN極側の寄与とS 極側の寄与の合計により磁場Bを求める事ができる。実際にはこの上下に現れた磁極面密度により磁石内部に－Z方向の磁界Hができる、これを反磁界と呼ぶ。磁石内部でのBdと反磁界Hdの比

$P c = \frac{B_{d}}{H_{d}}$

をパーミアンス係数と呼ぶ。パーミアンス係数は磁石の形状のみに依存する量であるが、磁石内部で必ずしも一定にはならない。ただN極とS極側の方向が長い形状の方が磁石の反磁界は磁極面から離れる為小さくなり、反磁界係数Pcは大きくなる。Fig.6に示した様に、あるパーミアンス係数Pcが与えられた時に、傾きが－Pcを持った直線を磁石の減磁曲線上に引いた時B-H曲線と直線の交点を磁石の動作点と呼びその磁石のB-H曲線上で磁石が使われているポイントを示している。

--------磁石専用磁場計算アプリケーション(Kojimag)に興味がある方はこちらへ--------

このサイトの基礎計算式を基に磁石専用アプリケーションを開発しました。
こちらから”磁石専用磁場計算アプリケーション(Kojimag)”からKojimagの詳細について確認できます。