§２０．一般角柱磁石の熱減磁

１）一般角柱磁石の熱減磁のモデル化

§18では、磁石の熱減磁について不可逆熱減磁量を温度と減磁曲線から定式化することができた。ここでは具体的に一般角柱磁石を考えその熱減磁の様子をモデル化する。

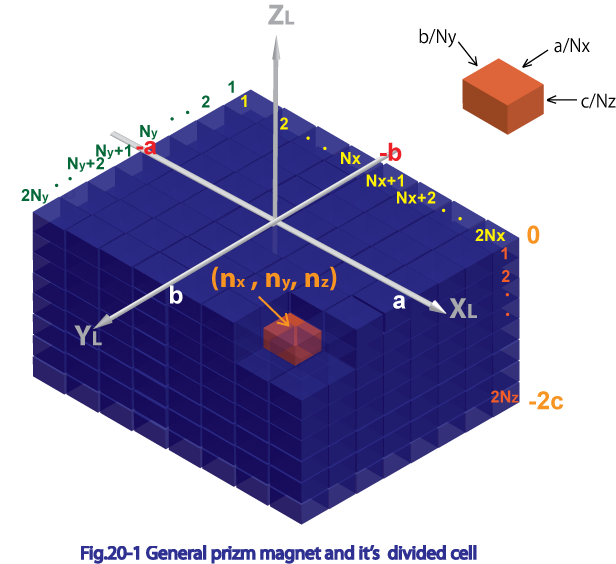
Fig.20-1に一般角柱磁石を示す。座標系は一般角柱磁石のローカル座標系 XL,YL,ZL で考える。各辺の長さは 2a,2b,2c とし、各辺を2Nx, 2Ny, 2Nz　等分に分割して考える。
分割された各セルの番号はXL,YL,ZL の各軸の方向で -a, -b, 0 の位置にあるセルを起点として各軸に番号付けするものとする。　nx, ny, nz 番目にあるセル（Fig20-1でオレンジ色のセル）の各辺の長さはa/Nx, b/Ny, c/Nz となり、また同セルの中心座標をCLnx, CLny, CLnz とすると　　

CLnx=-a+a/Nx ∙nx -a/Nx/2=a/Nxnx-Nx-1/2CLny=-b+b/Ny ∙ny-b/Ny/2=b/Nyny-Ny-1/2CLnz=-c/Nz ∙nz+c/Nz/2=-c/Nznz-1/2 式(20-1)

となる事が分かる。
全体座標系とローカル座標系の関係をFig.20-2に示す。一般角柱磁石は全体座標系で位置x, y, z にあり、全体座標系のX , Y, Z軸に対して角度 θx , θy, θzだけ回転しているものとする。

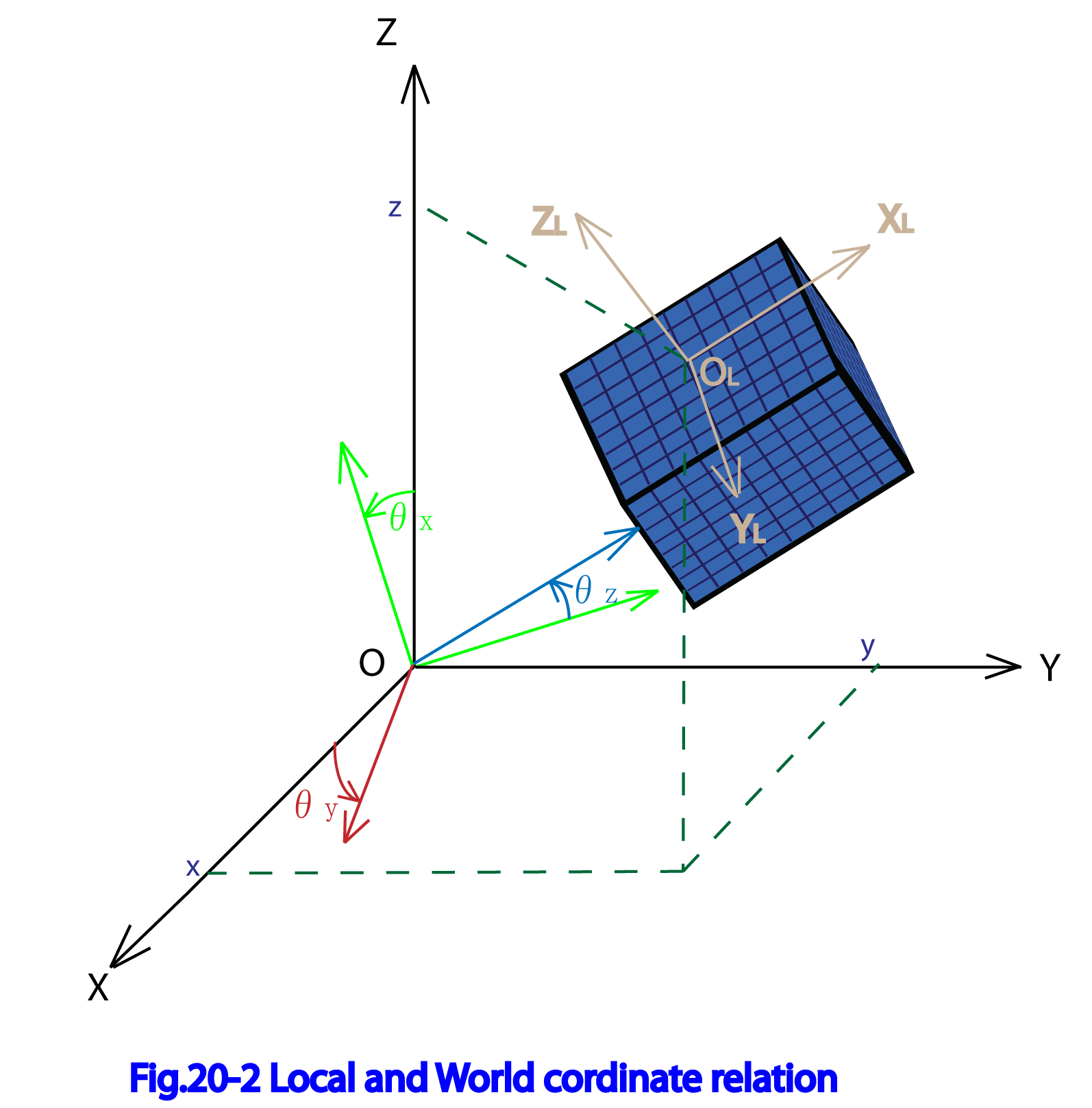
　そうすると、式(20-1 )のローカル座標値 CLnx, CLny, CLnz は§12の全体座標系と固有座標系式の関係の中の式(12-46)を参照して全体座標系では

Cnx, Cny, Cnz , 1=CLnx, CLny, CLnz , 1RzθzRy θyRx θxT( x , y, z) 式(20-2)

と表すことができる。

--------磁石専用磁場計算アプリケーション(Kojimag)に興味がある方はこちらへ--------

このサイトの基礎計算式を基に磁石専用アプリケーションを開発しました。
こちらから”磁石専用磁場計算アプリケーション(Kojimag)”からKojimagの詳細について確認できます。