§２０．一般角柱磁石の熱減磁 2）反磁界の計算

§２０．一般角柱磁石の熱減磁

２）各セルに働くの反磁界の計算

磁石の温度はT℃とする。§20-１）でモデル化した磁石の各セルの熱減磁率を§18の式(18-26)で表式化した値を用いて評価する。
各セルの熱減磁率は、先ず各セルの磁化が式(18-25)で表式化した温度Tにおける磁荷 $I (T)$ であるとしてローカル座標における各セルの中心座標の点 $(C_{L n_{x}}, C_{{Ln}_{y}}, C_{{Ln}_{z}})$ の反磁界からパーミアンス係数を式(19-4)から求める。
Fig.20-1に示した　 $(n_{x}, n_{y}, n_{z})$ 　番目にあるセルの中心座標の点における反磁界を考える。ローカル座標系で考える。 $(i , j , k)$ 番目のセルが $(n_{x}, n_{y}, n_{z})$ 　番目にあるセルの中心座標につくる磁界を　 $∆ {\overset{⃑}{H_{L}}}_{(i, j, k)} (n_{x}, n_{y}, n_{z})$ と表す。 $(i , j , k)$ 番目のセルの中心座標における磁化は、セルの温度をT℃として、磁化の向きは一般角柱磁石Fig.14-1に示したように極座標で $(φ, θ)$ の向きとし、ローカル座標系の各軸の単位ベクトルをe ${\overset{⃑}{e}}_{Lx}$ ${\overset{⃑}{e}}_{Ly}, {\overset{⃑}{e}}_{Lz}$ とすれば、式(18-25)より

${\overset{⃑}{I}}_{i , j , k} (T) = I_{20} [1 + \frac{C_{b r}}{100} (T - 20)] ({\sin θ \cos φ \overset{⃑}{e}}_{Lx} + \sin θ \sin φ {\overset{⃑}{e}}_{Ly} + {\cos θ \overset{⃑}{e}}_{Lz})$ 式(20-3)

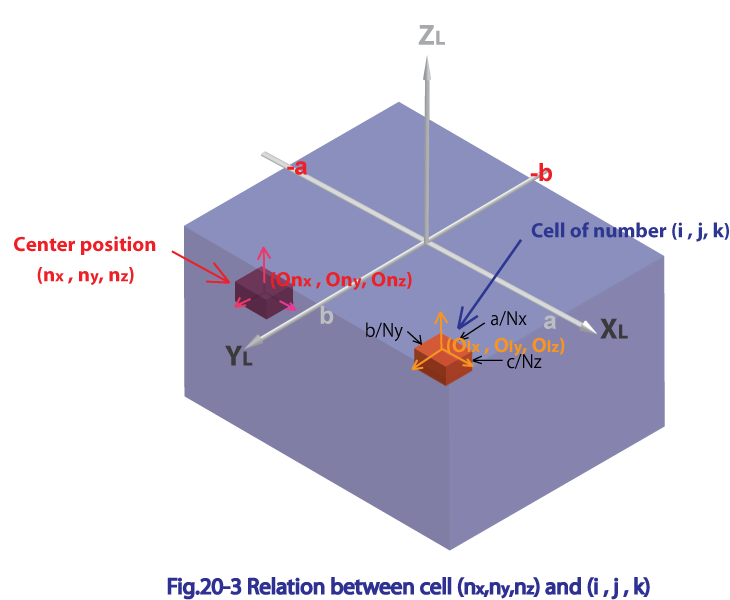
と表す事ができる。Fig.23-3に $(i , j , k)$ 番目のセルのローカル座標及び $(n_{x}, n_{y}, n_{z})$ 　番目にあるセルの中心座標の関係を図で示した。
$(n_{x}, n_{y}, n_{z})$ 番目のセルの中心座標は式(20-1)で表式化されている。また $(i , j , k)$ 番目のセルのローカル座標の原点は

$\begin{matrix} O_{lx} = a / N_{x} (i - N_{x} - \frac{1}{2}) \\ O_{ly} = b / N_{y} (j - N_{y} - \frac{1}{2}) \\ O_{lz} = - c / N_{z} (k - 1) \end{matrix}\}$ 式(20-4)

と表すことができるので $(i , j , k)$ 番目のセルのローカル座標からみた $(n_{x}, n_{y}, n_{z})$ 番目のセルの中心座標 $(O_{n_{x} i}, O_{n_{y} j}, O_{n_{z} k})$ は

$\begin{matrix} O_{n_{x} i} = C_{{Ln}_{x}} - O_{lx} = a / N_{x} (n_{x} - N_{x} - 1 / 2) - a / N_{x} (i - N_{x} - \frac{1}{2}) = a / N_{x} (n_{x} - i) \\ O_{n_{y} j} = C_{{Ln}_{y}} - O_{ly} = b / N_{y} (n_{y} - N_{y} - 1 / 2) - b / N_{y} (j - N_{y} - \frac{1}{2}) = b / N_{y} (n_{y} - j) \\ O_{n_{z} k} = C_{{Ln}_{y}} - O_{ly} = - c / N_{z} (n_{z} - 1 / 2) + c / N_{z} (k - 1) = - c / N_{z} (n_{z} - k+ \frac{1}{2}) \end{matrix}\}$ 式(20-5)

となる。

(nx,ny,nz)位置のセルと(ijk)の位置のセル関係

$(i , j , k)$ 　番目にあるセルのローカル座標を基準に考えれば、 $(i , j , k)$ 番目のセルが $(n_{x}, n_{y}, n_{z})$ 　番目にあるセルの中心座標につくる磁界　 $∆ {\overset{⃑}{H_{L}}}_{(i, j, k)} (n_{x}, n_{y}, n_{z})$ のｘ成分は　式(14-44)　において磁化M, 座標　 $(X_{0}, Y_{0}, Z_{0})$ ,及び磁石の各辺の長さとして以下の値

$\begin{matrix} M \to M_{i,j,k} = I_{20} [1 + \frac{C_{b r}}{100} (T - 20)] \\ X_{0} \to O_{n_{x} i} = a / N_{x} (n_{x} - i) \\ Y_{0} \to O_{n_{y} j} =b / N_{y} (n_{y} - j) \\ Z_{0} \to O_{n_{z} k} = - c / N_{z} (n_{z} - k+ \frac{1}{2}) \\ a \to a / (2 N_{x}) \\ b → b / (2 N_{y}) \\ c → c / (2 N_{z}) \end{matrix}\}$ 式(20-6)

を用いればよい。ここで　 $M_{i,j,k}$ 　は $(i , j , k)$ 番目のセルの磁化で、式(18-25) で表される。
即ち

${(∆ {\overset{⃑}{H_{L}}}_{(i, j, k)} (n_{x}, n_{y}, n_{z}))}_{x}$

$= \frac{I_{20} [1+ \frac{C_{br}}{100} (T-20)] cos θ}{4π μ_{0}} \log (\frac{[O_{n_{y} j} + b/ (2 N_{y})] + \sqrt{{[O_{n_{x} i} - a/ (2 N_{x})]}^{2} + {[O_{n_{y} j} + b/ (2 N_{y})]}^{2} + {O_{n_{z} k}}^{2}}}{[O_{n_{y} j} + b/ (2 N_{y})] + \sqrt{{{[O_{n_{x} i} + a/ (2 N_{x})]}^{2} + [O_{n_{y} j} + b/ (2 N_{y})]}^{2} + {O_{n_{z} k}}^{2}}}$

$\frac{[O_{n_{y} j} - b/ (2 N_{y})] + \sqrt{{[O_{n_{x} i} + a/ (2 N_{x})]}^{2} + {[O_{n_{y} j} - b/ (2 N_{y})]}^{2} + {O_{n_{z} k}}^{2}}}{[O_{n_{y} j} - b/ (2 N_{y})] + \sqrt{{[O_{n_{x} i} - a/ (2 N_{x})]}^{2} + {[O_{n_{y} j} - b/ (2 N_{y})]}^{2} + {O_{n_{z} k}}^{2}}})$

$+ \frac{I_{20} [1+ \frac{C_{br}}{100} (T-20)] sin θ sin φ}{4π μ_{0}} \log (\frac{(O_{n_{z} k} + \frac{c}{N_{z}}) + \sqrt{{(O_{n_{z} k} + \frac{c}{N_{z}})}^{2} + {[O_{n_{x} i} - \frac{a}{(2 N_{x})}]}^{2} + {[O_{n_{y} j} - b/ (2 N_{y})]}^{2}}}{(O_{n_{z} k} + \frac{c}{N_{z}}) + \sqrt{{{(O_{n_{z} k} + \frac{c}{N_{z}})}^{2} + [O_{n_{x} i} + \frac{a}{(2 N_{x})}]}^{2} + {[O_{n_{y} j} - b/ (2 N_{y})]}^{2}}}$

$\frac{O_{n_{z} k} + \sqrt{{{O_{n_{z} k}}^{2} + [O_{n_{x} i} + a/ (2 N_{x})]}^{2} + {[O_{n_{y} j} - b/ (2 N_{y})]}^{2}}}{O_{n_{z} k} + \sqrt{{{O_{n_{z} k}}^{2} + [O_{n_{x} i} - a/ (2 N_{x})]}^{2} + {[O_{n_{y} j} - b/ (2 N_{y})]}^{2}}})$

$+ \frac{I_{20} [1+ \frac{C_{br}}{100} (T-20)] sin θ cos φ}{4π μ_{0}} [\{\tan^{- 1} (\frac{1}{[O_{n_{x} i} - a/ (2 N_{x})]} \frac{[O_{n_{y} j} + b/ (2 N_{y})] (O_{n_{z} k} + \frac{c}{N_{z}})}{\sqrt{{[O_{n_{y} j} + b/ (2 N_{y})]}^{2} + {(O_{n_{z} k} + \frac{c}{N_{z}})}^{2} + {[O_{n_{x} i} - a/ (2 N_{x})]}^{2}}})$

$- \tan^{- 1} (\frac{1}{[O_{n_{x} i} - a/ (2 N_{x})]} \frac{[O_{n_{y} j} + b/ (2 N_{y})] O_{n_{z} k}}{\sqrt{{[O_{n_{y} j} + b/ (2 N_{y})]}^{2} + {O_{n_{z} k}}^{2} + {[O_{n_{x} i} - a/ (2 N_{x})]}^{2}}})\}$

$- \{\tan^{- 1} (\frac{1}{[O_{n_{x} i} - a/ (2 N_{x})]} \frac{[O_{n_{y} j} - b/ (2 N_{y})] (O_{n_{z} k} + \frac{c}{N_{z}})}{\sqrt{{[O_{n_{y} j} - b/ (2 N_{y})]}^{2} + {(O_{n_{z} k} + \frac{c}{N_{z}})}^{2} + {[O_{n_{x} i} - a/ (2 N_{x})]}^{2}}})$

$- \tan^{- 1} (\frac{1}{O_{n_{x} i} - a / (2 N_{x})} \frac{[O_{n_{y} j} - b/ (2 N_{y})] O_{n_{z} k}}{\sqrt{{[O_{n_{y} j} - b/ (2 N_{y})]}^{2} + {O_{n_{z} k}}^{2} + {[O_{n_{x} i} - a/ (2 N_{x})]}^{2}}})\}]$

$+ \frac{I_{20} [1+ \frac{C_{br}}{100} (T-20)] sin θ sin φ}{4π μ_{0}} \log (\frac{(O_{n_{z} k} + \frac{c}{N_{z}}) + \sqrt{{(O_{n_{z} k} + \frac{c}{N_{z}})}^{2} + {[O_{n_{x} i} - a/ (2 N_{x})]}^{2} + {[O_{n_{y} j} - b/ (2 N_{y})]}^{2}}}{(O_{n_{z} k} + \frac{c}{N_{z}}) + \sqrt{{{(O_{n_{z} k} + \frac{c}{N_{z}})}^{2} + [O_{n_{x} i} + a/ (2 N_{x})]}^{2} + {[O_{n_{y} j} - b/ (2 N_{y})]}^{2}}}$

$- \frac{I_{20} [1+ \frac{C_{br}}{100} (T-20)] sin θ cos φ}{4π μ_{0}} [\{\tan^{- 1} (\frac{1}{[O_{n_{x} i} + a/ (2 N_{x})]} \frac{[O_{n_{y} j} + b/ (2 N_{y})] (O_{n_{z} k} + \frac{c}{N_{z}})}{\sqrt{{[O_{n_{y} j} + b/ (2 N_{y})]}^{2} + {(O_{n_{z} k} + \frac{c}{N_{z}})}^{2} + {[O_{n_{x} i} + a/ (2 N_{x})]}^{2}}})$

$- \tan^{- 1} (\frac{1}{[O_{n_{x} i} + a/ (2 N_{x})]} \frac{[O_{n_{y} j} + b/ (2 N_{y})] O_{n_{z} k}}{\sqrt{{[O_{n_{y} j} + b/ (2 N_{y})]}^{2} + {O_{n_{z} k}}^{2} + {[O_{n_{x} i} + a/ (2 N_{x})]}^{2}}})\}$

$- \{\tan^{- 1} (\frac{1}{[O_{n_{x} i} + a/ (2 N_{x})]} \frac{[O_{n_{y} j} - b/ (2 N_{y})] (O_{n_{z} k} + \frac{c}{N_{z}})}{\sqrt{{[O_{n_{y} j} - b/ (2 N_{y})]}^{2} + {(O_{n_{z} k} + \frac{c}{N_{z}})}^{2} + {[O_{n_{x} i} + a/ (2 N_{x})]}^{2}}})$

$- \tan^{- 1} (\frac{1}{[O_{n_{x} i} + a/ (2 N_{x})]} \frac{[O_{n_{y} j} - b/ (2 N_{y})] O_{n_{z} k}}{\sqrt{{[O_{n_{y} j} - b/ (2 N_{y})]}^{2} + {O_{n_{z} k}}^{2} + {[O_{n_{x} i} + a/ (2 N_{x})]}^{2}}})\}]$

$- \frac{I_{20} [1+ \frac{C_{br}}{100} (T-20)] sin θ sin φ}{4π μ_{0}} l o g (\frac{(O_{n_{z} k} + \frac{c}{N_{z}}) + \sqrt{{(O_{n_{z} k} + \frac{c}{N_{z}})}^{2} + {[O_{n_{x} i} - a/ (2 N_{x})]}^{2} + {[O_{n_{y} j} + b/ (2 N_{y})]}^{2}}}{(O_{n_{z} k} + \frac{c}{N_{z}}) + \sqrt{{{(O_{n_{z} k} + \frac{c}{N_{z}})}^{2} + [O_{n_{x} i} + a/ (2 N_{x})]}^{2} + {[O_{n_{y} j} + b/ (2 N_{y})]}^{2}}}$

$\frac{O_{n_{z} k} + \sqrt{{{O_{n_{z} k}}^{2} + [O_{n_{x} i} + a/ (2 N_{x})]}^{2} + {[O_{n_{y} j} + b/ (2 N_{y})]}^{2}}}{O_{n_{z} k} + \sqrt{{{O_{n_{z} k}}^{2} + [O_{n_{x} i} - a/ (2 N_{x})]}^{2} + {[O_{n_{y} j} + b/ (2 N_{y})]}^{2}}})$

$- \frac{I_{20} [1+ \frac{C_{br}}{100} (T-20)] \cos θ}{4 π μ_{0}} \log (\frac{[O_{n_{y} j} + b/ (2 N_{y})] + \sqrt{{[O_{n_{x} i} - a/ (2 N_{x})]}^{2} + {[O_{n_{y} j} + b/ (2 N_{y})]}^{2} + {(O_{n_{z} k} + \frac{c}{N_{z}})}^{2}}}{[O_{n_{y} j} + b/ (2 N_{y})] + \sqrt{{{[O_{n_{x} i} + a/ (2 N_{x})]}^{2} + [O_{n_{y} j} + b/ (2 N_{y})]}^{2} + {(O_{n_{z} k} + \frac{c}{N_{z}})}^{2}}})$

$\frac{[O_{n_{y} j} - b/ (2 N_{y})] + \sqrt{{[O_{n_{x} i} + a/ (2 N_{x})]}^{2} + {[O_{n_{y} j} - b/ (2 N_{y})]}^{2} + {(O_{n_{z} k} + \frac{c}{N_{z}})}^{2}}}{[O_{n_{y} j} - b/ (2 N_{y})] + \sqrt{{[O_{n_{x} i} - a/ (2 N_{x})]}^{2} + {[O_{n_{y} j} - b/ (2 N_{y})]}^{2} + {(O_{n_{z} k} + \frac{c}{N_{z}})}^{2}}})$ 式(20-7)

次に　 $∆ {\overset{⃑}{H_{L}}}_{(i, j, k)} (n_{x}, n_{y}, n_{z})$ ) のｙ成分は　同様に式(14-45)において　式(20-6)　のように値を代入すればよく

${(∆ {\overset{⃑}{H_{L}}}_{(i, j, k)} (n_{x}, n_{y}, n_{z}))}_{y}$

$= \frac{I_{20} [1+ \frac{C_{br}}{100} (T-20)] \cos θ}{4 π μ_{0}} \log (\frac{[O_{n_{x} i} + a/ (2 N_{x})] + \sqrt{{[O_{n_{x} i} + a/ (2 N_{x})]}^{2} + {[O_{n_{y} j} - b/ (2 N_{y})]}^{2} + {O_{n_{z} k}}^{2}}}{[O_{n_{x} i} + a/ (2 N_{x})] + \sqrt{{{[O_{n_{x} i} + a/ (2 N_{x})]}^{2} + [O_{n_{y} j} + b/ (2 N_{y})]}^{2} + {O_{n_{z} k}}^{2}}}$

$\frac{[O_{n_{x} i} - a/ (2 N_{x})] + \sqrt{{{[O_{n_{x} i} - a/ (2 N_{x})]}^{2} + [O_{n_{y} j} + b/ (2 N_{y})]}^{2} + {O_{n_{z} k}}^{2}}}{[O_{n_{x} i} - a/ (2 N_{x})] + \sqrt{{{[O_{n_{x} i} - a/ (2 N_{x})]}^{2} + [O_{n_{y} j} - b/ (2 N_{y})]}^{2} + {O_{n_{z} k}}^{2}}})$

$+ \frac{I_{20} [1+ \frac{C_{br}}{100} (T-20)] sin θ cos φ}{4π μ_{0}} \log (\frac{O_{n_{z} k} + \frac{c}{N_{z}} + \sqrt{{[O_{n_{y} j} - b/ (2 N_{y})]}^{2} + {(O_{n_{z} k} + \frac{c}{N_{z}})}^{2} + {[O_{n_{x} i} - a/ (2 N_{x})]}^{2}}}{O_{n_{z} k} + \frac{c}{N_{z}} + \sqrt{{{[O_{n_{y} j} + b/ (2 N_{y})]}^{2} + (O_{n_{z} k} + \frac{c}{N_{z}})}^{2} + {[O_{n_{x} i} - a/ (2 N_{x})]}^{2}}}$

$\frac{O_{n_{z} k} + \sqrt{{[O_{n_{y} j} + b/ (2 N_{y})]}^{2} + {O_{n_{z} k}}^{2} + {[O_{n_{x} i} - a/ (2 N_{x})]}^{2}}}{O_{n_{z} k} + \sqrt{{[O_{n_{y} j} - b/ (2 N_{y})]}^{2} + {O_{n_{z} k}}^{2} + {[O_{n_{x} i} - a/ (2 N_{x})]}^{2}}})$

$+ \frac{I_{20} [1+ \frac{C_{br}}{100} (T-20)] sin θ sin φ}{4π μ_{0}} [\{\tan^{- 1} (\frac{1}{[O_{n_{y} j} - b/ (2 N_{y})]} \frac{(O_{n_{z} k} + \frac{c}{N_{z}}) [O_{n_{x} i} + a/ (2 N_{x})]}{\sqrt{{(O_{n_{z} k} + \frac{c}{N_{z}})}^{2} + {[O_{n_{x} i} + a/ (2 N_{x})]}^{2} + {[O_{n_{y} j} - b/ (2 N_{y})]}^{2}}})$

$- \tan^{- 1} (\frac{1}{[O_{n_{y} j} - b/ (2 N_{y})]} \frac{(O_{n_{z} k} + \frac{c}{N_{z}}) [O_{n_{x} i} - a/ (2 N_{x})]}{\sqrt{{(O_{n_{z} k} + \frac{c}{N_{z}})}^{2} + {[O_{n_{x} i} - a/ (2 N_{x})]}^{2} + {[O_{n_{y} j} - b/ (2 N_{y})]}^{2}}})\}$

$- \{\tan^{- 1} (\frac{1}{[O_{n_{y} j} - b/ (2 N_{y})]} \frac{O_{n_{z} k} [O_{n_{x} i} + a/ (2 N_{x})]}{\sqrt{{O_{n_{z} k}}^{2} + {[O_{n_{x} i} + a/ (2 N_{x})]}^{2} + {[O_{n_{y} j} - b/ (2 N_{y})]}^{2}}})$

$- \tan^{- 1} (\frac{1}{[O_{n_{y} j} - b/ (2 N_{y})]} \frac{O_{n_{z} k} [O_{n_{x} i} - a/ (2 N_{x})]}{\sqrt{{O_{n_{z} k}}^{2} + {[O_{n_{x} i} - a/ (2 N_{x})]}^{2} + {[O_{n_{y} j} - b/ (2 N_{y})]}^{2}}})\}]$

$- \frac{I_{20} [1+ \frac{C_{br}}{100} (T-20)] sin θ cos φ}{4π μ_{0}} \log (\frac{(O_{n_{z} k} + \frac{c}{N_{z}}) + \sqrt{{[O_{n_{y} j} - b/ (2 N_{y})]}^{2} + {(O_{n_{z} k} + \frac{c}{N_{z}})}^{2} + {[O_{n_{x} i} + a/ (2 N_{x})]}^{2}}}{(O_{n_{z} k} + \frac{c}{N_{z}}) + \sqrt{{{[O_{n_{y} j} + b/ (2 N_{y})]}^{2} + (O_{n_{z} k} + \frac{c}{N_{z}})}^{2} + {[O_{n_{x} i} + a/ (2 N_{x})]}^{2}}}$

$\frac{O_{n_{z} k} + \sqrt{{[O_{n_{y} j} + b/ (2 N_{y})]}^{2} + {O_{n_{z} k}}^{2} + {[O_{n_{x} i} + a/ (2 N_{x})]}^{2}}}{O_{n_{z} k} + \sqrt{{[O_{n_{y} j} - b/ (2 N_{y})]}^{2} + {O_{n_{z} k}}^{2} + {[O_{n_{x} i} + a/ (2 N_{x})]}^{2}}})$

$- \frac{I_{20} [1+ \frac{C_{br}}{100} (T-20)] sin θ sin φ}{4π μ_{0}} [\{\tan^{- 1} (\frac{1}{[O_{n_{y} j} + b/ (2 N_{y})]} \frac{(O_{n_{z} k} + \frac{c}{N_{z}}) [O_{n_{x} i} + a/ (2 N_{x})]}{\sqrt{{(O_{n_{z} k} + \frac{c}{N_{z}})}^{2} + {[O_{n_{x} i} + a/ (2 N_{x})]}^{2} + {[O_{n_{y} j} + b/ (2 N_{y})]}^{2}}})$

$- \tan^{- 1} (\frac{1}{[O_{n_{y} j} + b/ (2 N_{y})]} \frac{(O_{n_{z} k} + \frac{c}{N_{z}}) [O_{n_{x} i} - a/ (2 N_{x})]}{\sqrt{{(O_{n_{z} k} + \frac{c}{N_{z}})}^{2} + {[O_{n_{x} i} - a/ (2 N_{x})]}^{2} + {[O_{n_{y} j} + b/ (2 N_{y})]}^{2}}})\}$

$- \{\tan^{- 1} (\frac{1}{[O_{n_{y} j} + b/ (2 N_{y})]} \frac{O_{n_{z} k} [O_{n_{x} i} + a/ (2 N_{x})]}{\sqrt{{O_{n_{z} k}}^{2} + {[O_{n_{x} i} + a/ (2 N_{x})]}^{2} + {[O_{n_{y} j} + b/ (2 N_{y})]}^{2}}})$

$- \tan^{- 1} (\frac{1}{[O_{n_{y} j} + b/ (2 N_{y})]} \frac{O_{n_{z} k} [O_{n_{x} i} - a/ (2 N_{x})]}{\sqrt{{O_{n_{z} k}}^{2} + {[O_{n_{x} i} - a/ (2 N_{x})]}^{2} + {[O_{n_{y} j} + b/ (2 N_{y})]}^{2}}})\}]$

$- \frac{I_{20} [1+ \frac{C_{br}}{100} (T-20)] \cos θ}{4 π μ_{0}} \log (\frac{[O_{n_{x} i} + a/ (2 N_{x})] + \sqrt{{[O_{n_{x} i} + a/ (2 N_{x})]}^{2} + {[O_{n_{y} j} - b/ (2 N_{y})]}^{2} + {(O_{n_{z} k} + \frac{c}{N_{z}})}^{2}}}{[O_{n_{x} i} + a/ (2 N_{x})] + \sqrt{{{[O_{n_{x} i} + a/ (2 N_{x})]}^{2} + [O_{n_{y} j} + b/ (2 N_{y})]}^{2} + {(O_{n_{z} k} + \frac{c}{N_{z}})}^{2}}}$

$\frac{[O_{n_{x} i} - a/ (2 N_{x})] + \sqrt{{{[O_{n_{x} i} - a/ (2 N_{x})]}^{2} + [O_{n_{y} j} + b/ (2 N_{y})]}^{2} + {(O_{n_{z} k} + \frac{c}{N_{z}})}^{2}}}{[O_{n_{x} i} - a/ (2 N_{x})] + \sqrt{{{[O_{n_{x} i} - a/ (2 N_{x})]}^{2} + [O_{n_{y} j} - b/ (2 N_{y})]}^{2} + {(O_{n_{z} k} + \frac{c}{N_{z}})}^{2}}})$ 式(20-8)

最後に　 $∆ {\overset{⃑}{H_{L}}}_{(i, j, k)} (n_{x}, n_{y}, n_{z})$ のｚ成分は　同様に式(14-46)において　式(20-6)　のように値を代入すればよく

${(∆ {\overset{⃑}{H_{L}}}_{(i, j, k)} (n_{x}, n_{y}, n_{z}))}_{z}$

$= \frac{I_{20} [1+ \frac{C_{br}}{100} (T-20)] cos θ}{4π μ_{0}} [\{{tan}^{-1} (\frac{1}{O_{n_{z} k}} \frac{[O_{n_{x} i} + a/ (2 N_{x})] [O_{n_{y} j} + b/ (2 N_{y})]}{\sqrt{{[O_{n_{x} i} + a/ (2 N_{x})]}^{2} + {[O_{n_{y} j} + b/ (2 N_{y})]}^{2} + {O_{n_{z} k}}^{2}}})$

$- \tan^{- 1} (\frac{1}{O_{n_{z} k}} \frac{[O_{n_{x} i} + a/ (2 N_{x})] [O_{n_{y} j} - b/ (2 N_{y})]}{\sqrt{{[O_{n_{x} i} + a/ (2 N_{x})]}^{2} + {[O_{n_{y} j} - b/ (2 N_{y})]}^{2} + {O_{n_{z} k}}^{2}}})\}$

$- \{\tan^{- 1} (\frac{1}{O_{n_{z} k}} \frac{[O_{n_{x} i} - a/ (2 N_{x})] [O_{n_{y} j} + b/ (2 N_{y})]}{\sqrt{{[O_{n_{x} i} - a/ (2 N_{x})]}^{2} + {[O_{n_{y} j} + b/ (2 N_{y})]}^{2} + {O_{n_{z} k}}^{2}}})$

$- \tan^{- 1} (\frac{1}{O_{n_{z} k}} \frac{[O_{n_{x} i} - a/ (2 N_{x})] [O_{n_{y} j} - b/ (2 N_{y})]}{\sqrt{{[O_{n_{x} i} - a/ (2 N_{x})]}^{2} + {[O_{n_{y} j} - b/ (2 N_{y})]}^{2} + {O_{n_{z} k}}^{2}}})\}]$

$+ \frac{I_{20} [1 + \frac{C_{b r}}{100} (T - 20)] sin θ cos φ}{4π μ_{0}} \log (\frac{[O_{n_{y} j} + b/ (2 N_{y})] + \sqrt{{[O_{n_{y} j} + b/ (2 N_{y})]}^{2} + {Z_{0}}^{2} + {[O_{n_{x} i} - a/ (2 N_{x})]}^{2}}}{[O_{n_{y} j} + b/ (2 N_{y})] + \sqrt{{{[O_{n_{y} j} + b/ (2 N_{y})]}^{2} + (O_{n_{z} k} + \frac{c}{N_{z}})}^{2} + {[O_{n_{x} i} - a/ (2 N_{x})]}^{2}}}$

$\frac{[O_{n_{y} j} - b/ (2 N_{y})] + \sqrt{{{[O_{n_{y} j} - b/ (2 N_{y})]}^{2} + (O_{n_{z} k} + \frac{c}{N_{z}})}^{2} + {[O_{n_{x} i} - a/ (2 N_{x})]}^{2}}}{[O_{n_{y} j} - b/ (2 N_{y})] + \sqrt{{[O_{n_{y} j} - b/ (2 N_{y})]}^{2} + Z_{0}^{2} + {[O_{n_{x} i} - a/ (2 N_{x})]}^{2}}})$

$+ \frac{I_{20} [1 + \frac{C_{b r}}{100} (T - 20)] sin θ sin φ}{4π μ_{0}} \log (\frac{[O_{n_{x} i} + a/ (2 N_{x})] + \sqrt{{Z_{0}}^{2} + {[O_{n_{x} i} + a/ (2 N_{x})]}^{2} + {[O_{n_{y} j} - b/ (2 N_{y})]}^{2}}}{[O_{n_{x} i} + a/ (2 N_{x})] + \sqrt{{{(O_{n_{z} k} + \frac{c}{N_{z}})}^{2} + [O_{n_{x} i} + a/ (2 N_{x})]}^{2} + {[O_{n_{y} j} - b/ (2 N_{y})]}^{2}}}$

$\frac{[O_{n_{x} i} - a/ (2 N_{x})] + \sqrt{{(O_{n_{z} k} + \frac{c}{N_{z}})}^{2} + {[O_{n_{x} i} - a/ (2 N_{x})]}^{2} + {[O_{n_{y} j} - b/ (2 N_{y})]}^{2}}}{[O_{n_{x} i} - a/ (2 N_{x})] + \sqrt{{Z_{0}}^{2} + {[O_{n_{x} i} - a/ (2 N_{x})]}^{2} + {[O_{n_{y} j} - b/ (2 N_{y})]}^{2}}})$

$- \frac{I_{20} [1 + \frac{C_{b r}}{100} (T - 20)] sin θ cos φ}{4π μ_{0}} \log (\frac{[O_{n_{y} j} + b/ (2 N_{y})] + \sqrt{{[O_{n_{y} j} + b/ (2 N_{y})]}^{2} + {Z_{0}}^{2} + {[O_{n_{x} i} + a/ (2 N_{x})]}^{2}}}{[O_{n_{y} j} + b/ (2 N_{y})] + \sqrt{{{[O_{n_{y} j} + b/ (2 N_{y})]}^{2} + (O_{n_{z} k} + \frac{c}{N_{z}})}^{2} + {[O_{n_{x} i} + a/ (2 N_{x})]}^{2}}}$

$\frac{[O_{n_{y} j} - b/ (2 N_{y})] + \sqrt{{{[O_{n_{y} j} - b/ (2 N_{y})]}^{2} + (O_{n_{z} k} + \frac{c}{N_{z}})}^{2} + {[O_{n_{x} i} + a/ (2 N_{x})]}^{2}}}{[O_{n_{y} j} - b/ (2 N_{y})] + \sqrt{{[O_{n_{y} j} - b/ (2 N_{y})]}^{2} + Z_{0}^{2} + {[O_{n_{x} i} + a/ (2 N_{x})]}^{2}}})$

$- \frac{I_{20} [1 + \frac{C_{b r}}{100} (T - 20)] sin θ sin φ}{4π μ_{0}} \log (\frac{[O_{n_{x} i} + a/ (2 N_{x})] + \sqrt{{Z_{0}}^{2} + {[O_{n_{x} i} + a/ (2 N_{x})]}^{2} + {[O_{n_{y} j} + b/ (2 N_{y})]}^{2}}}{[O_{n_{x} i} + a/ (2 N_{x})] + \sqrt{{{(O_{n_{z} k} + \frac{c}{N_{z}})}^{2} + [O_{n_{x} i} + a/ (2 N_{x})]}^{2} + {[O_{n_{y} j} + b/ (2 N_{y})]}^{2}}}$

$\frac{[O_{n_{x} i} - a/ (2 N_{x})] + \sqrt{{(O_{n_{z} k} + \frac{c}{N_{z}})}^{2} + {[O_{n_{x} i} - a/ (2 N_{x})]}^{2} + {[O_{n_{y} j} + b/ (2 N_{y})]}^{2}}}{[O_{n_{x} i} - a/ (2 N_{x})] + \sqrt{{Z_{0}}^{2} + {[O_{n_{x} i} - a/ (2 N_{x})]}^{2} + {[O_{n_{y} j} + b/ (2 N_{y})]}^{2}}})$

$- \frac{I_{20} [1 + \frac{C_{b r}}{100} (T - 20)] \cos θ}{4 π μ_{0}} [\{\tan^{- 1} (\frac{1}{(O_{n_{z} k} + \frac{c}{N_{z}})} \frac{[O_{n_{x} i} + a/ (2 N_{x})] [O_{n_{y} j} + b/ (2 N_{y})]}{\sqrt{{[O_{n_{x} i} + a/ (2 N_{x})]}^{2} + {[O_{n_{y} j} + b/ (2 N_{y})]}^{2} + {(O_{n_{z} k} + \frac{c}{N_{z}})}^{2}}})$

$- \tan^{- 1} (\frac{1}{(O_{n_{z} k} + \frac{c}{N_{z}})} \frac{[O_{n_{x} i} + a/ (2 N_{x})] [O_{n_{y} j} - b/ (2 N_{y})]}{\sqrt{{[O_{n_{x} i} + a/ (2 N_{x})]}^{2} + {[O_{n_{y} j} - b/ (2 N_{y})]}^{2} + {(O_{n_{z} k} + \frac{c}{N_{z}})}^{2}}})\}$

$- \{{tan}^{-1} (\frac{1}{(O_{n_{z} k} + \frac{c}{N_{z}})} \frac{[O_{n_{x} i} -a/ (2 N_{x})] [O_{n_{y} j} + b/ (2 N_{y})]}{\sqrt{{[O_{n_{x} i} -a/ (2 N_{x})]}^{2} + {[O_{n_{y} j} + b/ (2 N_{y})]}^{2} + {(O_{n_{z} k} + \frac{c}{N_{z}})}^{2}}})$

$- \tan^{- 1} (\frac{1}{(O_{n_{z} k} + \frac{c}{N_{z}})} \frac{[O_{n_{x} i} - a/ (2 N_{x})] [O_{n_{y} j} - b/ (2 N_{y})]}{\sqrt{{[O_{n_{x} i} - a/ (2 N_{x})]}^{2} + {[O_{n_{y} j} - b/ (2 N_{y})]}^{2} + {(O_{n_{z} k} + \frac{c}{N_{z}})}^{2}}})\}]$ 式(20-9)

式(20-7), (20-8) , (20-9)より $(n_{x}, n_{y}, n_{z})$ 　番目にあるセルの中心座標につくる磁界は　 $∆ {\overset{⃑}{H_{L}}}_{(i, j, k)} (n_{x}, n_{y}, n_{z})$ 　の $(i , j , k)$ 　に関して総和を求めればよく

${\overset{⃑}{H}}_{n_{x}, n_{y}, n_{z}} (T) = \sum_{i =1}^{2 N_{x}} \sum_{j=1}^{2 N_{y}} \sum_{k=1}^{2 N_{z}} \{{(∆ {\overset{⃑}{H_{L}}}_{(i, j, k)} (n_{x}, n_{y}, n_{z}))}_{x} {\overset{⃑}{e}}_{Lx} + {(∆ {\overset{⃑}{H_{L}}}_{(i, j, k)} (n_{x}, n_{y}, n_{z}))}_{x} {\overset{⃑}{e}}_{L y}$

${+ (∆ {\overset{⃑}{H_{L}}}_{(i, j, k)} (n_{x}, n_{y}, n_{z}))}_{x} {\overset{⃑}{e}}_{L y}\}$ 式(20-10)

として求めることができた。

--------磁石専用磁場計算アプリケーション(Kojimag)に興味がある方はこちらへ--------

このサイトの基礎計算式を基に磁石専用アプリケーションを開発しました。
こちらから”磁石専用磁場計算アプリケーション(Kojimag)”からKojimagの詳細について確認できます。

公開日：2015年5月4日　　　　　　更新日：2023年10月16日　　　　
作成者：児島　伸生
連絡先：
2011-2023 Copyright by Kojimag