§4　三角型磁極　1)磁界の表式

§４．三角型磁極により作られる磁界

1)磁界の表式

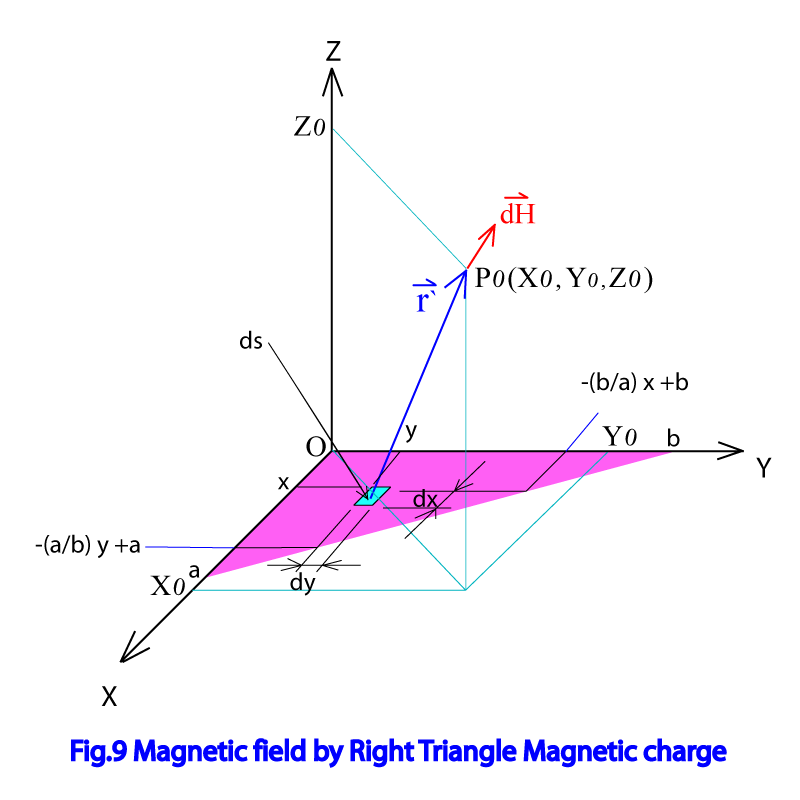
Fig.9で示されるように固有座標径に於いて、X 軸方向の長さが a、Y 軸方向の長さが b の三角形の磁極面が点 $P_{0} (X_{0}, Y_{0}, Z_{0})$ に作る磁界を計算する。磁極表面の磁化MはZ軸方向を向いているとする。

点（x , y , 0）に位置し、微小 X 方向長さdx、微小 Y 方向長さdyを持った微小要素をds　とする。　座標原点O からdsまでのベクトル $\overset{⃑}{r}$ 及び dsの面積は、

$\overset{⃑}{r} = (x, y, 0)$

$d s = d x d y$ 式(4-1)

となる。また、dsから点 $P_{0}$ 迄を結んだベクトルを $\overset{⃑}{r `}$ とすると、

$\overset{⃑}{r `} = \overset{⃑}{P_{0}} - \overset{⃑}{r} = (X_{0} － x, Y_{0} － y, Z_{0})$ 式(4-2)

となり、距離　r` は

$r ` = \sqrt{\overset{⃑}{r `} ∙ \overset{⃑}{r `}} = \sqrt{({X_{0} － x)}^{2} + {{(Y}_{0} － y)}^{2} + {Z_{0}}^{2}}$ 式(4-3)

となる。

また微小要素の磁極面の磁荷　dm は、磁石の残留磁束密度を　Br　とすると、

$d m = B r d s = B r d x d y$

と表せる。

微小要素dsによって点 $P_{0}$ に作られる磁界 $\overset{⃑}{d H}$ はdsから点 $P_{0}$ を結ぶ方向を向いたベクトルで以下の様に表せる。

$\overset{⃑}{d H} = \frac{d m}{4 π μ_{0} {r `}^{2}} \frac{\overset{⃑}{r `}}{r `} = \frac{B r d x d y}{4 π μ_{0} {r `}^{2}} \frac{\overset{⃑}{r `}}{r `}$

従って、全ての三角形磁極面からの磁界 $\overset{⃑}{H}$ への寄与は三角形全体のXとyに関して積分する事により求められる。その際積分の順序と範囲に注意する。

$\overset{⃑}{H} = \iint \overset{⃑}{d H} = \frac{B r}{4 π μ_{0}} \int_{0}^{b} (\int_{0}^{- \frac{a}{b} y + a} \frac{1}{{r `}^{2}} \frac{\overset{⃑}{r `}}{r `} d x) d y$ 又は、

$= \frac{B r}{4 π μ_{0}} \int_{0}^{a} (\int_{0}^{- \frac{b}{a} x + b} \frac{1}{{r `}^{2}} \frac{\overset{⃑}{r `}}{r `} d y) d x$

と表せる。　 $\vec{r^{`}}$ 　の　式(4-2）を用いて　 $\overset{⃑}{H}$ 　の各成分で表す。その際 Hx は xの積分、Hy は yの積分を先に行う。

$H x = \frac{B r}{4 π μ_{0}} \int_{0}^{b} (\int_{0}^{- \frac{a}{b} y + a} \frac{1}{{r `}^{3}} (X_{0} - x) d x) d y$ 式(4-4)

$H_{y} = \frac{B r}{4 π μ_{0}} \int_{0}^{a} (\int_{0}^{- \frac{b}{a} x + b} \frac{1}{{r `}^{3}} (Y_{0} - y) d y) d x$ 式(4-5)

$H_{Z} = \frac{B r}{4 π μ_{0}} \int_{0}^{a} (\int_{0}^{- \frac{b}{a} x + b} \frac{1}{{r `}^{3}} Z_{0} d y) d x$ 式(4-6)

となる。

ここで、式(4-4) , (4-5)　において夫々　 $X_{0} - x = t$ , $Y_{0} - y = u$ , とおくと式(4-4)、(4-5)の積分範囲は夫々　 $[X_{0}, X_{0} - (- \frac{a}{b} y + a)]$ 　, $[Y_{0}, Y_{0} - (- \frac{b}{a} x + b)]$ 　となり、-dx=dt , -dy=du であるので　式(4-4)、(4-5)　は

$H x = \frac{B r}{4 π μ_{0}} \int_{0}^{b} \{\int_{X_{0} - a (1 - \frac{y}{b})}^{X_{0}} \frac{t d t}{{\sqrt{t^{2} + {{(Y}_{0} － y)}^{2} + {Z_{0}}^{2}}}^{3}}\} d y$ 式(4-4')

$H y = \frac{B r}{4 π μ_{0}} \int_{0}^{a} \{\int_{Y_{0} - b (1 - \frac{x}{a})}^{Y_{0}} \frac{u d u}{{\sqrt{({X_{0} － x)}^{2} + u^{2} + {Z_{0}}^{2}}}^{3}}\} d x$ 式(4-5')

とt 又はu に関する積分で表せる。　

--------磁石専用磁場計算アプリケーション(Kojimag)に興味がある方はこちらへ--------

このサイトの基礎計算式を基に磁石専用アプリケーションを開発しました。
こちらから”磁石専用磁場計算アプリケーション(Kojimag)”からKojimagの詳細について確認できます。