§5　円形磁極　1)磁界の表式

§５．円形磁極面により作られる磁界

1)磁界の表式

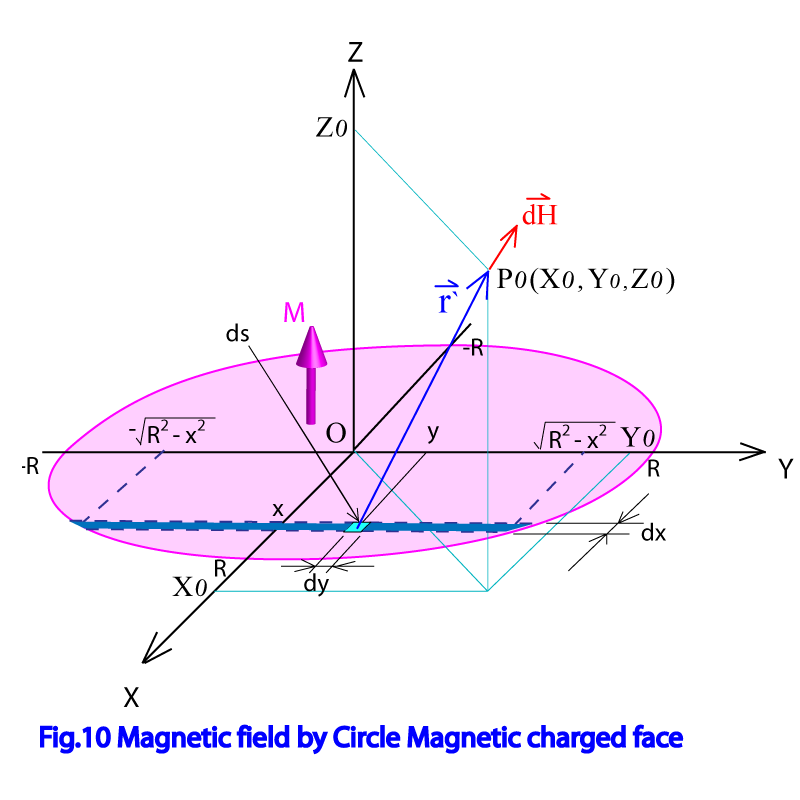
Fig.10で示されたように固有座標径に於いて、半径Rの磁極面が点　 $P_{0} (X_{0}, Y_{0,} Z_{0})$ 　に作る磁界を計算する。磁極表面の磁化MはZ軸方向を向いているとする。X座標がxからdxの幅を持った帯状の磁極面が点 $P_{0} (X_{0}, Y_{0,} Z_{0})$ に作る磁場は、微小X方向長さdx、微小Y方向長さdyを持った微小要素をds　とするとその面積は、

ds= dx dy 式(5-1)

となり、また、dsから点 $P_{0}$ 迄を結んだベクトルを　 $\overset{⃑}{r `}$ 　とすると、

$\overset{⃑}{r `} = (X_{0} - x, Y_{0} - y, Z_{0})$ 式(5-2)

となり、距離　r` は

$r ` = \sqrt{\overset{⃑}{r `} ･ \overset{⃑}{r `}} = \sqrt{({X_{0} － x)}^{2} + {{(Y}_{0} － y)}^{2} + {Z_{0}}^{2}}$ 式(5-3)

と現わす事ができる。微小要素の磁化dmは磁石の残留磁束密度をBrとすると

$d m = B r d s = B r d x d y$ 式(5-4)

である。またこの微小磁化が点 $P_{0}$ に作る磁界 $\overset{⃑}{d H}$ は

$\overset{⃑}{d H} ＝ \frac{d m}{4 π μ_{0}} \frac{1}{{r^{'}}^{2}} \frac{\overset{⃑}{r^{'}}}{r^{'}}$ 式(5-5)

と表せるので、X座標がxからdxの幅を持った帯状の磁極面が点 $P_{0} (X_{0}, Y_{0}, Z_{0})$ に作る磁場は式(5-5)をY座標が $- \sqrt{R^{2} - x^{2}}$ 　から $\sqrt{R^{2} - x^{2}}$ 　迄積分すればよく

$\int_{- \sqrt{R^{2} - x^{2}}}^{\sqrt{R^{2} - x^{2}}} (\frac{B r}{4 π μ_{0}} \frac{1}{{r^{'}}^{2}} \frac{\overset{⃑}{r^{'}}}{r^{'}} d y) d x$ 式(5-6)

と表される。円形の磁極面全体が点 $P_{0} (X_{0}, Y_{0}, Z_{0})$ に作る磁界は式(5-6)をXについて－RからR迄積分する事によって求められるので

$\overset{⃑}{H} = \frac{B r}{4 π μ_{0}} \int_{- R}^{R} \{\int_{- \sqrt{R^{2} - x^{2}}}^{\sqrt{R^{2} - x^{2}}} (\frac{1}{{r^{'}}^{2}} \frac{\overset{⃑}{r^{'}}}{r^{'}} d y) d x\}$ 式(5-7)

となる。式(5-2)及び式(5-3)を用いると式(5-7)の $\overset{⃑}{H}$ の各成分は

$\begin{matrix} H_{x} = \frac{B r}{4 π μ_{0}} \int_{- R}^{R} [\int_{- \sqrt{R^{2} - x^{2}}}^{\sqrt{R^{2} - x^{2}}} (\frac{X_{0} － x}{{r^{'}}^{3}} d y) d x] \\ H_{y} = \frac{B r}{4 π μ_{0}} \int_{- R}^{R} [\int_{- \sqrt{R^{2} - x^{2}}}^{\sqrt{R^{2} - x^{2}}} (\frac{Y_{0} － y}{{r^{'}}^{3}} d y) d x] \\ H_{z} = \frac{B r}{4 π μ_{0}} \int_{- R}^{R} [\int_{- \sqrt{R^{2} - x^{2}}}^{\sqrt{R^{2} - x^{2}}} (\frac{Z_{0}}{{r^{'}}^{3}} d y) d x] \end{matrix}\}$ 式(5-8)

と表す事ができる。

--------磁石専用磁場計算アプリケーション(Kojimag)に興味がある方はこちらへ--------

このサイトの基礎計算式を基に磁石専用アプリケーションを開発しました。
こちらから”磁石専用磁場計算アプリケーション(Kojimag)”からKojimagの詳細について確認できます。