§９．扇型平角ワイヤーに流れる電流要素により作られる磁界 1)磁界の表式

§９．扇型平角ワイヤーに流れる電流により作られる磁界

1)磁界の表式

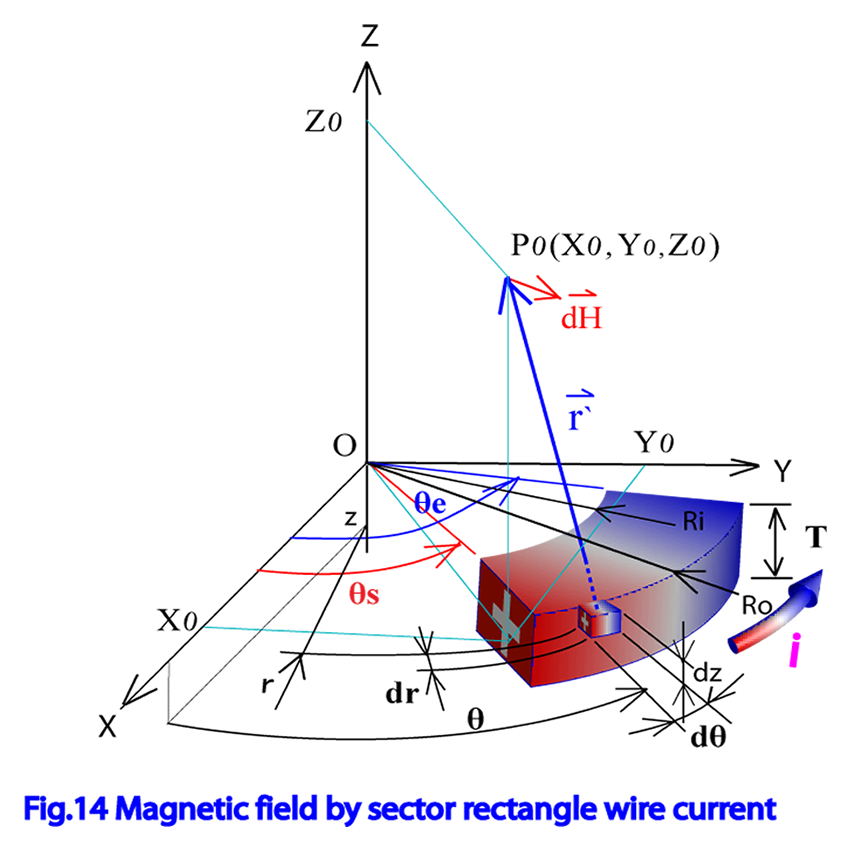
扇型平角導線に流れる電流により作られる磁場

Fig.14に示したように固有座標系　X-Y-Z おいて内径がRi　外径がRo、厚さがT、開始角度がθsから終了角度がθe までで定義された扇形平角導線に角度方向に電流密度ｉの電流が流れている時に、点 $P (X_{0}, Y_{0}, Z_{0})$ に作られる磁界を表式化する。扇形平角導線内の微小電流要素はFig.14に示したように円柱座標系で位置（ｒ, θ , z ）に大きさ（dr, dθ ,dz ) の微小広がりで定義されているものとする。また導線の上面が固有座標系のZ=0　の面と一致するものとする。

この微小電流要素が点 $P_{0}$ に作る磁界はビオサバールの法則により

$\overset{⃑}{d H} = \frac{1}{4 π} \frac{i ∙ d r ∙ d z ∙ (r d θ {\overset{⃑}{e}}_{θ}) \times \overset{⃑}{r'}}{{r'}^{3}}$ 式(9-1)

ここで $\overset{⃑}{r'}$ は微小電流要素から点 $P_{0}$ へのベクトルで ${\overset{⃑}{e}}_{θ}$ は角度 θ における接線方向の単位ベクトルとする。（Fig.15参照）微小電流要素の位置は X-Y-Z座標系だと $(r ∙ \cos θ, r ∙ \sin θ, z)$ であるから

$\overset{⃑}{r'} = (X_{0} - r ∙ \cos θ, Y_{0} - r ∙ \sin θ, Z_{0} - z)$

従って外積　 ${\overset{⃑}{e}}_{θ} \times \overset{⃑}{r'}$ は

${\overset{⃑}{e}}_{θ} \times \overset{⃑}{r'} ＝ (\cos θ ∙ (Z_{0} - z), \sin θ ∙ (Z_{0} - z), - \sin θ (Y_{0} - r ∙ \sin θ) - \cos θ (X_{0} - r ∙ \cos θ))$ 式(9-2)

よって式(9-1)は

$\begin{matrix} {d H}_{x} = \frac{1}{4 π} \frac{1}{{r'}^{3}} i r d r d θ d z \cos θ (Z_{0} - z) \\ {d H}_{y} = \frac{1}{4 π} \frac{1}{{r'}^{3}} i r d r d θ d z \sin θ (Z_{0} - z) \\ {d H}_{z} = \frac{1}{4 π} \frac{1}{{r'}^{3}} i r d r d θ d z [- \sin θ (Y_{0} - r ∙ \sin θ) - \cos θ (X_{0} - r ∙ \cos θ)] \end{matrix}\}$ 式(9-3)

ここで $r^{'}$ = $\sqrt{{(X_{0} - r ∙ \cos θ)}^{2} + {(Y_{0} - r ∙ \sin θ)}^{2} + {(Z_{0} - z)}^{2}}$

と表せる。Hx　,Hy,　Hz　は式(9-3)をr　,　 θ　,　z　に関してコイルの全範囲に渡って積分する事によって求める事ができ

$\begin{matrix} H_{x} = \frac{i}{4 π} \int_{R_{i}}^{R_{o}} r d r \int_{θ_{s}}^{θ_{e}} \cos θ d θ \int_{- T}^{0} \frac{Z_{0} - z}{{\sqrt{{(X_{0} - r ∙ \cos θ)}^{2} + {(Y_{0} - r ∙ \sin θ)}^{2} + {(Z_{0} - z)}^{2}}}^{3}} d z \\ H_{y} = \frac{i}{4 π} \int_{R_{i}}^{R_{o}} r d r \int_{θ_{s}}^{θ_{e}} \sin θ d θ \int_{- T}^{0} \frac{Z_{0} - z}{{\sqrt{{(X_{0} - r ∙ \cos θ)}^{2} + {(Y_{0} - r ∙ \sin θ)}^{2} + {(Z_{0} - z)}^{2}}}^{3}} d z \\ H_{z} = \frac{i}{4 π} \int_{R_{i}}^{R_{o}} r d r \int_{θ_{s}}^{θ_{e}} d θ \int_{- T}^{0} \frac{- \sin θ (Y_{0} - r ∙ \sin θ) - \cos θ (X_{0} - r ∙ \cos θ)}{{\sqrt{{(X_{0} - r ∙ \cos θ)}^{2} + {(Y_{0} - r ∙ \sin θ)}^{2} + {(Z_{0} - z)}^{2}}}^{3}} d z \end{matrix}\}$ 式(9-4)

と表せる。

--------磁石専用磁場計算アプリケーション(Kojimag)に興味がある方はこちらへ--------

このサイトの基礎計算式を基に磁石専用アプリケーションを開発しました。
こちらから”磁石専用磁場計算アプリケーション(Kojimag)”からKojimagの詳細について確認できます。